**Converting Radians to Degrees** To convert an angle from radians to degrees, use the following formula: \[ \text{Degrees} = \text{Radians} \times \frac{180}{\pi} \] Let's apply this formula to the given problem: ### Problem Convert the angle in radians to degrees. Given: \[ \frac{14\pi}{9} \text{ radians} \] ### Solution 1. **Multiply by the Conversion Factor:** \[ \text{Degrees} = \frac{14\pi}{9} \times \frac{180}{\pi} \] 2. **Simplify the Expression:** \[ \text{Degrees} = \frac{14 \times 180}{9} \] 3. **Calculate the Result:** \[ \text{Degrees} = \frac{2520}{9} = 280^\circ \] Therefore, \(\frac{14\pi}{9}\) radians is equal to \(280^\circ\). ### Explanation - **Conversion Factor**: We use \(\frac{180}{\pi}\) because \(180^\circ\) is equivalent to \(\pi\) radians. - **Simplification**: \(\pi\) in the numerator and denominator cancels out, simplifying calculation. - **Calculation**: Perform arithmetic to find the degree measure. This approach helps in converting any radian measurement into degrees effortlessly.
**Converting Radians to Degrees** To convert an angle from radians to degrees, use the following formula: \[ \text{Degrees} = \text{Radians} \times \frac{180}{\pi} \] Let's apply this formula to the given problem: ### Problem Convert the angle in radians to degrees. Given: \[ \frac{14\pi}{9} \text{ radians} \] ### Solution 1. **Multiply by the Conversion Factor:** \[ \text{Degrees} = \frac{14\pi}{9} \times \frac{180}{\pi} \] 2. **Simplify the Expression:** \[ \text{Degrees} = \frac{14 \times 180}{9} \] 3. **Calculate the Result:** \[ \text{Degrees} = \frac{2520}{9} = 280^\circ \] Therefore, \(\frac{14\pi}{9}\) radians is equal to \(280^\circ\). ### Explanation - **Conversion Factor**: We use \(\frac{180}{\pi}\) because \(180^\circ\) is equivalent to \(\pi\) radians. - **Simplification**: \(\pi\) in the numerator and denominator cancels out, simplifying calculation. - **Calculation**: Perform arithmetic to find the degree measure. This approach helps in converting any radian measurement into degrees effortlessly.
Calculus: Early Transcendentals
8th Edition
ISBN:9781285741550
Author:James Stewart
Publisher:James Stewart
Chapter1: Functions And Models
Section: Chapter Questions
Problem 1RCC: (a) What is a function? What are its domain and range? (b) What is the graph of a function? (c) How...
Related questions
Question
![**Converting Radians to Degrees**
To convert an angle from radians to degrees, use the following formula:
\[ \text{Degrees} = \text{Radians} \times \frac{180}{\pi} \]
Let's apply this formula to the given problem:
### Problem
Convert the angle in radians to degrees.
Given:
\[ \frac{14\pi}{9} \text{ radians} \]
### Solution
1. **Multiply by the Conversion Factor:**
\[
\text{Degrees} = \frac{14\pi}{9} \times \frac{180}{\pi}
\]
2. **Simplify the Expression:**
\[
\text{Degrees} = \frac{14 \times 180}{9}
\]
3. **Calculate the Result:**
\[
\text{Degrees} = \frac{2520}{9} = 280^\circ
\]
Therefore, \(\frac{14\pi}{9}\) radians is equal to \(280^\circ\).
### Explanation
- **Conversion Factor**: We use \(\frac{180}{\pi}\) because \(180^\circ\) is equivalent to \(\pi\) radians.
- **Simplification**: \(\pi\) in the numerator and denominator cancels out, simplifying calculation.
- **Calculation**: Perform arithmetic to find the degree measure.
This approach helps in converting any radian measurement into degrees effortlessly.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fcd2dd931-1327-4f45-b811-57e34410e87f%2F54197cb5-9941-4169-9a90-075325d003f0%2Fkkqj8vs.jpeg&w=3840&q=75)
Transcribed Image Text:**Converting Radians to Degrees**
To convert an angle from radians to degrees, use the following formula:
\[ \text{Degrees} = \text{Radians} \times \frac{180}{\pi} \]
Let's apply this formula to the given problem:
### Problem
Convert the angle in radians to degrees.
Given:
\[ \frac{14\pi}{9} \text{ radians} \]
### Solution
1. **Multiply by the Conversion Factor:**
\[
\text{Degrees} = \frac{14\pi}{9} \times \frac{180}{\pi}
\]
2. **Simplify the Expression:**
\[
\text{Degrees} = \frac{14 \times 180}{9}
\]
3. **Calculate the Result:**
\[
\text{Degrees} = \frac{2520}{9} = 280^\circ
\]
Therefore, \(\frac{14\pi}{9}\) radians is equal to \(280^\circ\).
### Explanation
- **Conversion Factor**: We use \(\frac{180}{\pi}\) because \(180^\circ\) is equivalent to \(\pi\) radians.
- **Simplification**: \(\pi\) in the numerator and denominator cancels out, simplifying calculation.
- **Calculation**: Perform arithmetic to find the degree measure.
This approach helps in converting any radian measurement into degrees effortlessly.
Expert Solution
Step 1
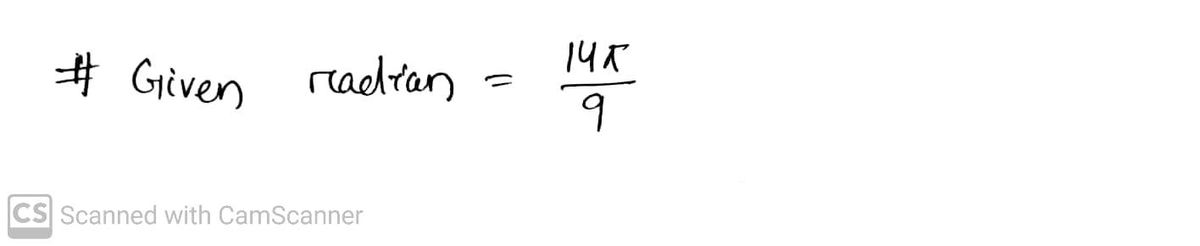
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781319050740
Author:
Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:
W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:
9781337552516
Author:
Ron Larson, Bruce H. Edwards
Publisher:
Cengage Learning