Homework Help is Here – Start Your Trial Now!
Math
Calculus
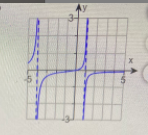
**Graph Analysis of a Rational Function** **Instruction:** Use the graph of the rational function to complete the following statement. **Statement:** As \( x \to -4^- \), \( f(x) \to \, \_\_\_\_ \) **Graph Description:** - The graph displays a rational function with a vertical asymptote at \( x = -4 \). - As \( x \) approaches \(-4\) from the left (\(x \to -4^-\)), the graph shows that \( f(x) \) tends towards negative infinity, i.e., \( f(x) \to -\infty \). - There is another vertical asymptote at \( x = 3 \). - The horizontal asymptote appears to be the x-axis (\(y = 0\)). **Answer Box:** As \( x \to -4^- \), \( f(x) \to -\infty \). **Instruction for Submission:** Enter your answer in the answer box and then click "Check Answer." **Note:** This exercise helps in understanding the behavior of rational functions near their asymptotes and the concept of limits.

**Graph Analysis of a Rational Function** **Instruction:** Use the graph of the rational function to complete the following statement. **Statement:** As \( x \to -4^- \), \( f(x) \to \, \_\_\_\_ \) **Graph Description:** - The graph displays a rational function with a vertical asymptote at \( x = -4 \). - As \( x \) approaches \(-4\) from the left (\(x \to -4^-\)), the graph shows that \( f(x) \) tends towards negative infinity, i.e., \( f(x) \to -\infty \). - There is another vertical asymptote at \( x = 3 \). - The horizontal asymptote appears to be the x-axis (\(y = 0\)). **Answer Box:** As \( x \to -4^- \), \( f(x) \to -\infty \). **Instruction for Submission:** Enter your answer in the answer box and then click "Check Answer." **Note:** This exercise helps in understanding the behavior of rational functions near their asymptotes and the concept of limits.

Calculus: Early Transcendentals
Calculus: Early Transcendentals
8th Edition
ISBN:9781285741550
Author:James Stewart
Publisher:James Stewart
Chapter1: Functions And Models
Section: Chapter Questions
Problem 1RCC: (a) What is a function? What are its domain and range? (b) What is the graph of a function? (c) How...
See similar textbooks
icon
Related questions
Question
**Graph Analysis of a Rational Function** **Instruction:** Use the graph of the rational function to complete the following statement. **Statement:** As \( x \to -4^- \), \( f(x) \to \, \_\_\_\_ \) **Graph Description:** - The graph displays a rational function with a vertical asymptote at \( x = -4 \). - As \( x \) approaches \(-4\) from the left (\(x \to -4^-\)), the graph shows that \( f(x) \) tends towards negative infinity, i.e., \( f(x) \to -\infty \). - There is another vertical asymptote at \( x = 3 \). - The horizontal asymptote appears to be the x-axis (\(y = 0\)). **Answer Box:** As \( x \to -4^- \), \( f(x) \to -\infty \). **Instruction for Submission:** Enter your answer in the answer box and then click "Check Answer." **Note:** This exercise helps in understanding the behavior of rational functions near their asymptotes and the concept of limits.
Transcribed Image Text:**Graph Analysis of a Rational Function** **Instruction:** Use the graph of the rational function to complete the following statement. **Statement:** As \( x \to -4^- \), \( f(x) \to \, \_\_\_\_ \) **Graph Description:** - The graph displays a rational function with a vertical asymptote at \( x = -4 \). - As \( x \) approaches \(-4\) from the left (\(x \to -4^-\)), the graph shows that \( f(x) \) tends towards negative infinity, i.e., \( f(x) \to -\infty \). - There is another vertical asymptote at \( x = 3 \). - The horizontal asymptote appears to be the x-axis (\(y = 0\)). **Answer Box:** As \( x \to -4^- \), \( f(x) \to -\infty \). **Instruction for Submission:** Enter your answer in the answer box and then click "Check Answer." **Note:** This exercise helps in understanding the behavior of rational functions near their asymptotes and the concept of limits.
Expert Solution
Step 1

Given

Calculus homework question answer, step 1, image 1

steps

Step by step

Solved in 2 steps with 1 images

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer
Recommended textbooks for you
Calculus: Early Transcendentals
Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning
Thomas' Calculus (14th Edition)
Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON
Calculus: Early Transcendentals (3rd Edition)
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON
Calculus: Early Transcendentals
Calculus: Early Transcendentals
Calculus
ISBN:
9781319050740
Author:
Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:
W. H. Freeman
Precalculus
Precalculus
Calculus
ISBN:
9780135189405
Author:
Michael Sullivan
Publisher:
PEARSON
Calculus: Early Transcendental Functions
Calculus: Early Transcendental Functions
Calculus
ISBN:
9781337552516
Author:
Ron Larson, Bruce H. Edwards
Publisher:
Cengage Learning
SEE MORE TEXTBOOKS