This image contains a mathematical expression involving a triple integral, which can be seen transcribed below: \[ \int_{2}^{6} \int_{1}^{4-y} \int_{0}^{12-3y-3z} \frac{1}{y} \, dx \, dz \, dy \] ### Explanation: This is a triple integral, often used to calculate the volume under a surface in three-dimensional space. Here's a breakdown of each part: - **Integral Limits**: - The outermost integral with respect to \( y \) has limits from 2 to 6. - The middle integral with respect to \( z \) has limits from 1 to \( 4-y \). - The innermost integral with respect to \( x \) has limits from 0 to \( 12-3y-3z \). - **Integrand**: - The expression being integrated is \( \frac{1}{y} \). - **Order of Integration**: - The integration proceeds from the innermost to the outermost integral, i.e., first with respect to \( x \), then \( z \), and finally \( y \). This integral setup implies a region bounded by specified planes and surfaces in 3D space, and the result represents a volume or accumulated quantity over this region.
This image contains a mathematical expression involving a triple integral, which can be seen transcribed below: \[ \int_{2}^{6} \int_{1}^{4-y} \int_{0}^{12-3y-3z} \frac{1}{y} \, dx \, dz \, dy \] ### Explanation: This is a triple integral, often used to calculate the volume under a surface in three-dimensional space. Here's a breakdown of each part: - **Integral Limits**: - The outermost integral with respect to \( y \) has limits from 2 to 6. - The middle integral with respect to \( z \) has limits from 1 to \( 4-y \). - The innermost integral with respect to \( x \) has limits from 0 to \( 12-3y-3z \). - **Integrand**: - The expression being integrated is \( \frac{1}{y} \). - **Order of Integration**: - The integration proceeds from the innermost to the outermost integral, i.e., first with respect to \( x \), then \( z \), and finally \( y \). This integral setup implies a region bounded by specified planes and surfaces in 3D space, and the result represents a volume or accumulated quantity over this region.
Calculus: Early Transcendentals
8th Edition
ISBN:9781285741550
Author:James Stewart
Publisher:James Stewart
Chapter1: Functions And Models
Section: Chapter Questions
Problem 1RCC: (a) What is a function? What are its domain and range? (b) What is the graph of a function? (c) How...
Related questions
Question
![This image contains a mathematical expression involving a triple integral, which can be seen transcribed below:
\[
\int_{2}^{6} \int_{1}^{4-y} \int_{0}^{12-3y-3z} \frac{1}{y} \, dx \, dz \, dy
\]
### Explanation:
This is a triple integral, often used to calculate the volume under a surface in three-dimensional space. Here's a breakdown of each part:
- **Integral Limits**:
- The outermost integral with respect to \( y \) has limits from 2 to 6.
- The middle integral with respect to \( z \) has limits from 1 to \( 4-y \).
- The innermost integral with respect to \( x \) has limits from 0 to \( 12-3y-3z \).
- **Integrand**:
- The expression being integrated is \( \frac{1}{y} \).
- **Order of Integration**:
- The integration proceeds from the innermost to the outermost integral, i.e., first with respect to \( x \), then \( z \), and finally \( y \).
This integral setup implies a region bounded by specified planes and surfaces in 3D space, and the result represents a volume or accumulated quantity over this region.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fd9f391b6-5f04-4d98-9bc5-d57c88046352%2F14a4b1c0-14a6-4a76-b1a1-7e1dee01937a%2F2qosx_processed.jpeg&w=3840&q=75)
Transcribed Image Text:This image contains a mathematical expression involving a triple integral, which can be seen transcribed below:
\[
\int_{2}^{6} \int_{1}^{4-y} \int_{0}^{12-3y-3z} \frac{1}{y} \, dx \, dz \, dy
\]
### Explanation:
This is a triple integral, often used to calculate the volume under a surface in three-dimensional space. Here's a breakdown of each part:
- **Integral Limits**:
- The outermost integral with respect to \( y \) has limits from 2 to 6.
- The middle integral with respect to \( z \) has limits from 1 to \( 4-y \).
- The innermost integral with respect to \( x \) has limits from 0 to \( 12-3y-3z \).
- **Integrand**:
- The expression being integrated is \( \frac{1}{y} \).
- **Order of Integration**:
- The integration proceeds from the innermost to the outermost integral, i.e., first with respect to \( x \), then \( z \), and finally \( y \).
This integral setup implies a region bounded by specified planes and surfaces in 3D space, and the result represents a volume or accumulated quantity over this region.
Expert Solution
Step 1
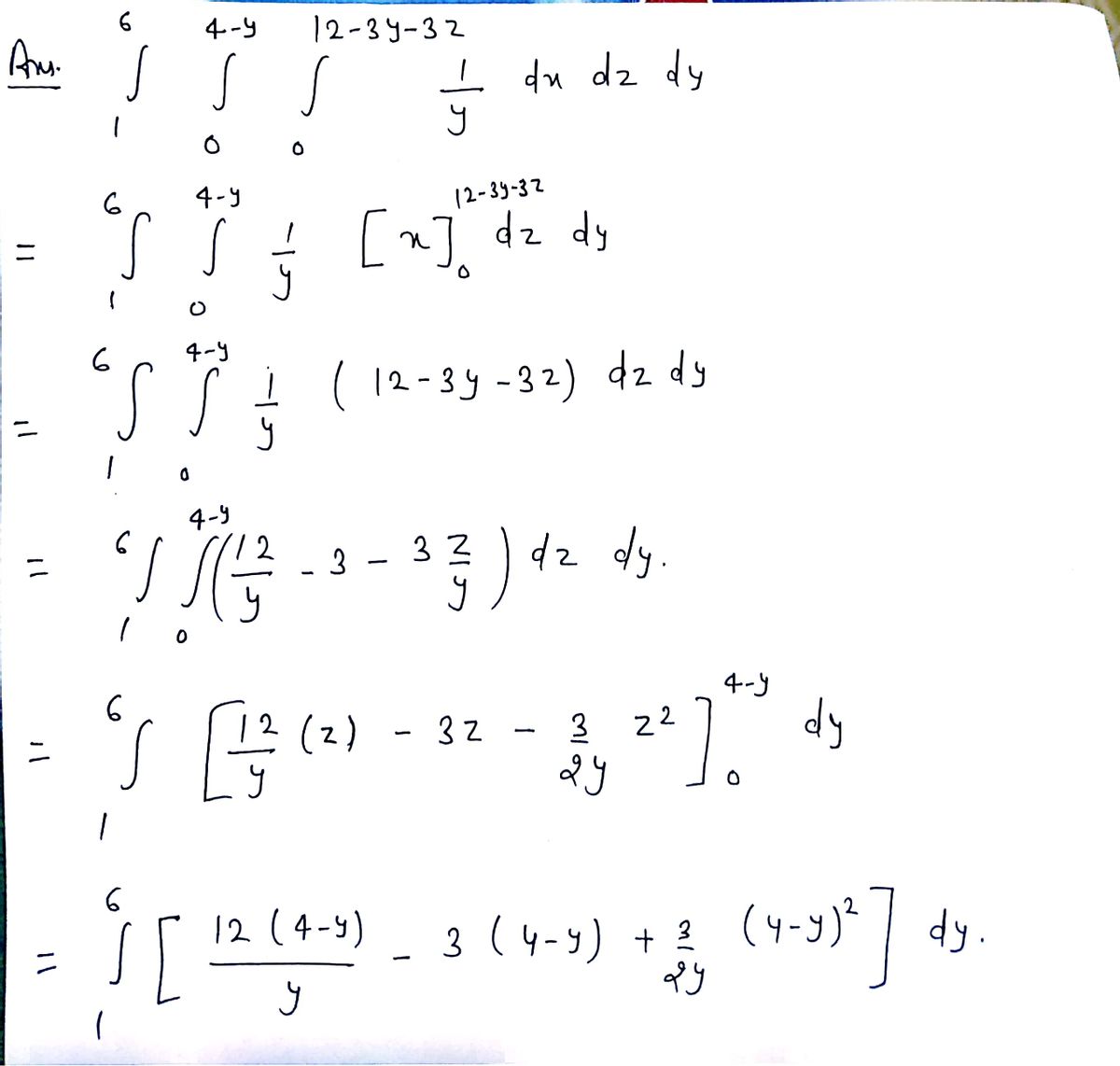
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781319050740
Author:
Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:
W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:
9781337552516
Author:
Ron Larson, Bruce H. Edwards
Publisher:
Cengage Learning