Calculate the derivative of the function. HINT [See Example 1.] f(x) = (x⁹-x)⁹ Step 1 Recall the Chain Rule. If f is a differentiable function of u and u is a differentiable function of x, then the composite f(u) is a differentiable function of x, and d 1 [f(u)] = f'(U). dx du Many like to think of the derivative of f(expression) as the derivative of f of the expression times the derivative of the expression. For the function f(x) = (x³ - x)³, note that f is a composite function with an expression that is raised to a power. Hence, the Generalized Power Rule,[u] = nu" - 1 du find the derivative of f. If we think of (x²-x) as u, then u is a differentiable function Apply the Generalized Power Rule to find the derivative of uº. = [4²] = ( f'(x) = x and u = dx' will be used to
Calculate the derivative of the function. HINT [See Example 1.] f(x) = (x⁹-x)⁹ Step 1 Recall the Chain Rule. If f is a differentiable function of u and u is a differentiable function of x, then the composite f(u) is a differentiable function of x, and d 1 [f(u)] = f'(U). dx du Many like to think of the derivative of f(expression) as the derivative of f of the expression times the derivative of the expression. For the function f(x) = (x³ - x)³, note that f is a composite function with an expression that is raised to a power. Hence, the Generalized Power Rule,[u] = nu" - 1 du find the derivative of f. If we think of (x²-x) as u, then u is a differentiable function Apply the Generalized Power Rule to find the derivative of uº. = [4²] = ( f'(x) = x and u = dx' will be used to
Calculus: Early Transcendentals
8th Edition
ISBN:9781285741550
Author:James Stewart
Publisher:James Stewart
Chapter1: Functions And Models
Section: Chapter Questions
Problem 1RCC: (a) What is a function? What are its domain and range? (b) What is the graph of a function? (c) How...
Related questions
Question
![Calculate the derivative of the function. HINT [See Example 1.]
\[ f(x) = (x^9 - x)^9 \]
### Step 1
**Recall the Chain Rule.**
If \( f \) is a differentiable function of \( u \) and \( u \) is a differentiable function of \( x \), then the composite \( f(u) \) is a differentiable function of \( x \), and
\[ \frac{d}{dx} [f(u)] = f'(u) \cdot \frac{du}{dx} \]
Many like to think of the derivative of \( f(\text{expression}) \) as the derivative of \( f \) of the expression times the derivative of the expression.
For the function \( f(x) = (x^9 - x)^9 \), note that \( f \) is a composite function with an expression that is raised to a power. Hence, the Generalized Power Rule,
\[ \frac{d}{dx}[u^n] = nu^{n-1} \frac{du}{dx} \]
will be used to find the derivative of \( f \).
If we think of \( (x^9 - x)^9 \) as \( u^9 \), then \( u \) is a differentiable function of \( x \) and \( u = \)
[Text Box]
Apply the Generalized Power Rule to find the derivative of \( u^9 \).
\[ f'(x) = \frac{d}{dx} [u^9] \]
\[ = \left( \rule{3cm}{0.15mm} \right) u^8 \frac{du}{dx} \]](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fd48171ba-d1cc-47b1-bf9c-8041143384f0%2Fa6b4769d-eeb1-40c8-82b8-c72eb785ac11%2F4gbajr_processed.png&w=3840&q=75)
Transcribed Image Text:Calculate the derivative of the function. HINT [See Example 1.]
\[ f(x) = (x^9 - x)^9 \]
### Step 1
**Recall the Chain Rule.**
If \( f \) is a differentiable function of \( u \) and \( u \) is a differentiable function of \( x \), then the composite \( f(u) \) is a differentiable function of \( x \), and
\[ \frac{d}{dx} [f(u)] = f'(u) \cdot \frac{du}{dx} \]
Many like to think of the derivative of \( f(\text{expression}) \) as the derivative of \( f \) of the expression times the derivative of the expression.
For the function \( f(x) = (x^9 - x)^9 \), note that \( f \) is a composite function with an expression that is raised to a power. Hence, the Generalized Power Rule,
\[ \frac{d}{dx}[u^n] = nu^{n-1} \frac{du}{dx} \]
will be used to find the derivative of \( f \).
If we think of \( (x^9 - x)^9 \) as \( u^9 \), then \( u \) is a differentiable function of \( x \) and \( u = \)
[Text Box]
Apply the Generalized Power Rule to find the derivative of \( u^9 \).
\[ f'(x) = \frac{d}{dx} [u^9] \]
\[ = \left( \rule{3cm}{0.15mm} \right) u^8 \frac{du}{dx} \]
Expert Solution
Step 1
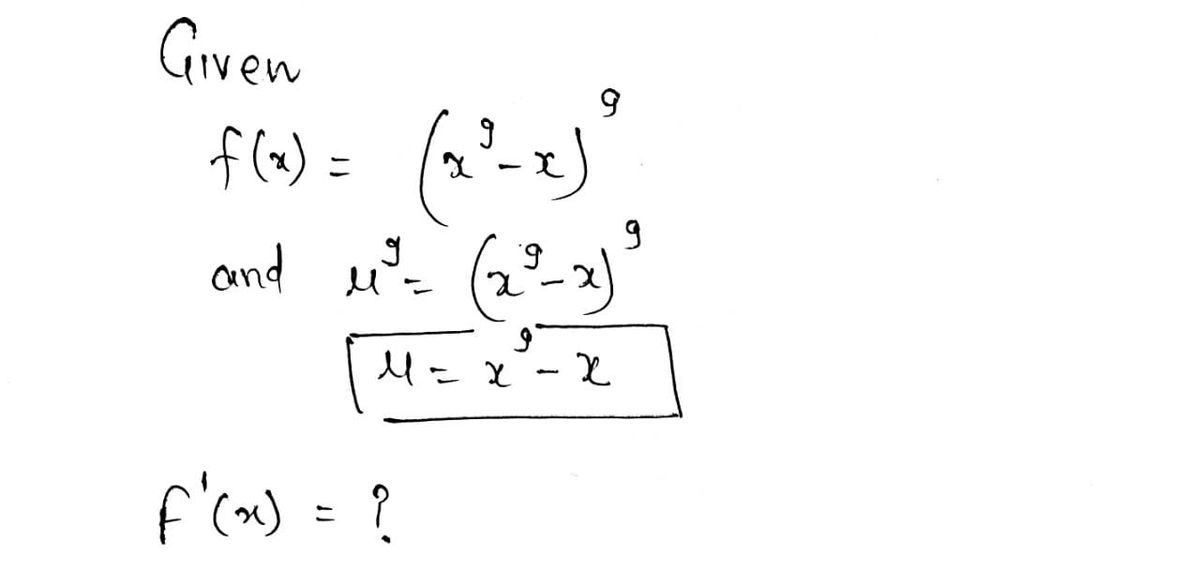
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781319050740
Author:
Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:
W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:
9781337552516
Author:
Ron Larson, Bruce H. Edwards
Publisher:
Cengage Learning