c) …more than 16.50 ounces? d) …between 16.20 and 16.26 ounces?
The labels on boxes of Cheesy Poofs say that the box contains 16 ounces of Cheesy Poofs, but that doesn’t
guarantee that each box contains exactly 16.00 ounces. The machine that fills the boxes doesn’t always
put out the exact same amount. The amount in each box is
deviation is .40 ounces. To help assure that most boxes contain as much or more than the label says, the
machine is set so that the mean will be 16.28 ounces. If you purchase 6 boxes of Cheesy Poofs,
find the
c) …more than 16.50 ounces?
d) …between 16.20 and 16.26 ounces?
The Z-score of a random variable X is defined as follows:
Here, µ and σ are the mean and standard deviation of X, respectively.
Consider a random variable x̅ that defines the average amount.
According to the given information X follows normal distribution with mean 16.28 ounces and standard deviation 0.40 ounces. The sample size, n is 6.
c)
The standard error of the mean is:
To find the probability that the average amount in 6 boxes is more than 16.50 ounces:
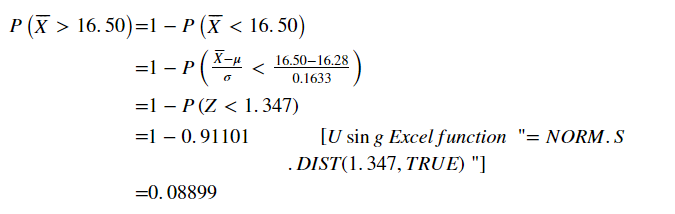
using a standard normal table, look up for z-score 1.35 corresponding probability is 0.91149
Then, subtract the value from total probability 1. Since, we need area to the right of z-score.
Therefore, probability that the average amount in 6 boxes is more than 16.50 ounces is 0.089
Step by step
Solved in 2 steps with 1 images
