by the equations { L₁ : X Y Let L₁ and L2 be lines in a 3-dimensional space given { = = Z = 3 + 2t 1+t - 2 - 3t and L₂: X Y Z = = = t -4 + 4t 1 Does L₁ and L2 intersect? Describe the intersection. Find an equation of the plane containing L₁ and L2.
by the equations { L₁ : X Y Let L₁ and L2 be lines in a 3-dimensional space given { = = Z = 3 + 2t 1+t - 2 - 3t and L₂: X Y Z = = = t -4 + 4t 1 Does L₁ and L2 intersect? Describe the intersection. Find an equation of the plane containing L₁ and L2.
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
![Let \( L_1 \) and \( L_2 \) be lines in a 3-dimensional space given by the equations
\[
L_1 :
\begin{cases}
x = 3 + 2t \\
y = 1 + t \\
z = -2 - 3t
\end{cases}
\qquad \text{and} \qquad
L_2 :
\begin{cases}
x = t \\
y = -4 + 4t \\
z = 1
\end{cases}
\]
Does \( L_1 \) and \( L_2 \) intersect? Describe the intersection. Find an equation of the plane containing \( L_1 \) and \( L_2 \).](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F3ef06bb3-2d9b-4f27-bb3b-835b443ab608%2F69e7c69e-5d12-4fc5-8163-45d2c83a9245%2Fotfz00w_processed.jpeg&w=3840&q=75)
Transcribed Image Text:Let \( L_1 \) and \( L_2 \) be lines in a 3-dimensional space given by the equations
\[
L_1 :
\begin{cases}
x = 3 + 2t \\
y = 1 + t \\
z = -2 - 3t
\end{cases}
\qquad \text{and} \qquad
L_2 :
\begin{cases}
x = t \\
y = -4 + 4t \\
z = 1
\end{cases}
\]
Does \( L_1 \) and \( L_2 \) intersect? Describe the intersection. Find an equation of the plane containing \( L_1 \) and \( L_2 \).
Expert Solution
Step 1: Given lines
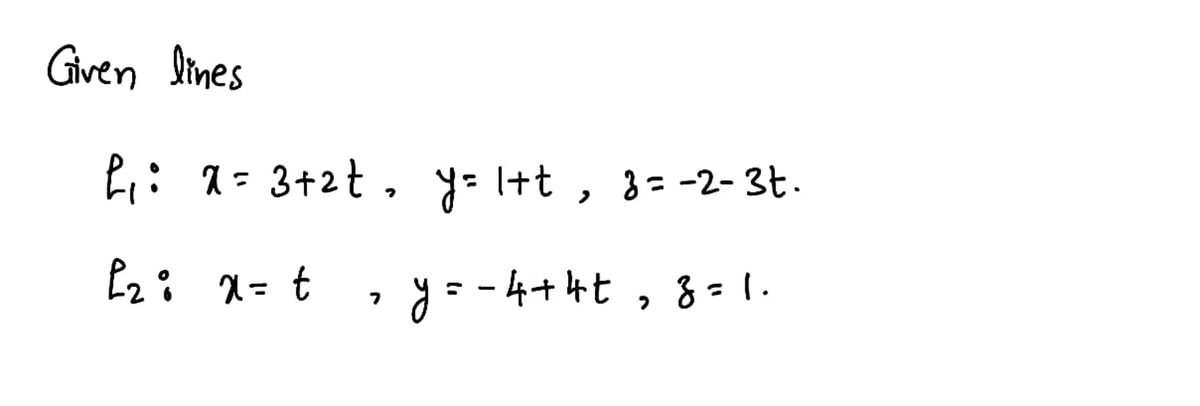
Step by step
Solved in 3 steps with 3 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

