boundad by the Genera te by revolving the cura Y=tan X Cand the y -axis X= Gabout

Hi! You have posted multiple questions. As per norms, we will be solving only one question. We will be solving the first one as nothing is specified. If you need the answer to other sub-parts then kindly re-submit the question by specifying the required sub-part.
We need to find the volume of the solid generated by revolving the region bounded by the curve y = tan x and x = π/4 about the y-axis.
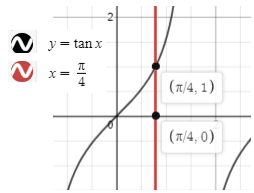
The graphical representation of the solid is given by along with intersecting points is,
 .
.
Here, radius = x and y is ranging from 0 to 1 which can be observed from the graph.
The integral form is,
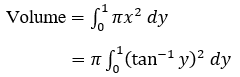
For the above integration, we will have to take the help of numerical methods. Thus, by the washer method or disk method, the finding volume becomes complicated. Thus, now we will be using the shell method.
We have the radius = x, height = y, and the thickness = dy. And the range of y is from 0 to 1.
So, the integral form is,
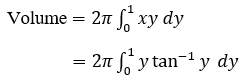 .
.
Step by step
Solved in 3 steps with 4 images









