Below are four pairs of functions, labeled f and g. For each, determine constants a and no such that for all n > no, a· f(n) > g(n). Give a clear argument as to why your choice of no and a satisfy the conditions. а. f(n) — 2n + 3, g(n) — 5n b. f(n) = 2n + 3, g(n) = 5n + log(n) c. f(n) = n'/4, g(n) = log(n) %3D d. f(n) = n, g(n) = (log2 n)ª
Below are four pairs of functions, labeled f and g. For each, determine constants a and no such that for all n > no, a· f(n) > g(n). Give a clear argument as to why your choice of no and a satisfy the conditions. а. f(n) — 2n + 3, g(n) — 5n b. f(n) = 2n + 3, g(n) = 5n + log(n) c. f(n) = n'/4, g(n) = log(n) %3D d. f(n) = n, g(n) = (log2 n)ª
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
Can someone help me with part d?

Transcribed Image Text:**Part 3: Big-Oh? K.**
**Suggested reading:** Sections 2.1 and 2.2 of *Algorithm Design*.
Below are four pairs of functions, labeled \( f \) and \( g \). For each, determine constants \( a \) and \( n_0 \) such that for all \( n \geq n_0 \), \( a \cdot f(n) \geq g(n) \). Give a clear argument as to why your choice of \( n_0 \) and \( a \) satisfy the conditions.
**a.** \( f(n) = 2n + 3, \, g(n) = 5n \)
**b.** \( f(n) = 2n + 3, \, g(n) = 5n + \log(n) \)
**c.** \( f(n) = n^{1/4}, \, g(n) = \log(n) \)
**d.** \( f(n) = n, \, g(n) = (\log_2 n)^4 \)
**e.** \( f(n) = n^3, \, g(n) = 6n + 1 \)
**Hint:** you may assume that for all \( x > 0 \), \( \log(x) < x \).
Expert Solution
Step 1
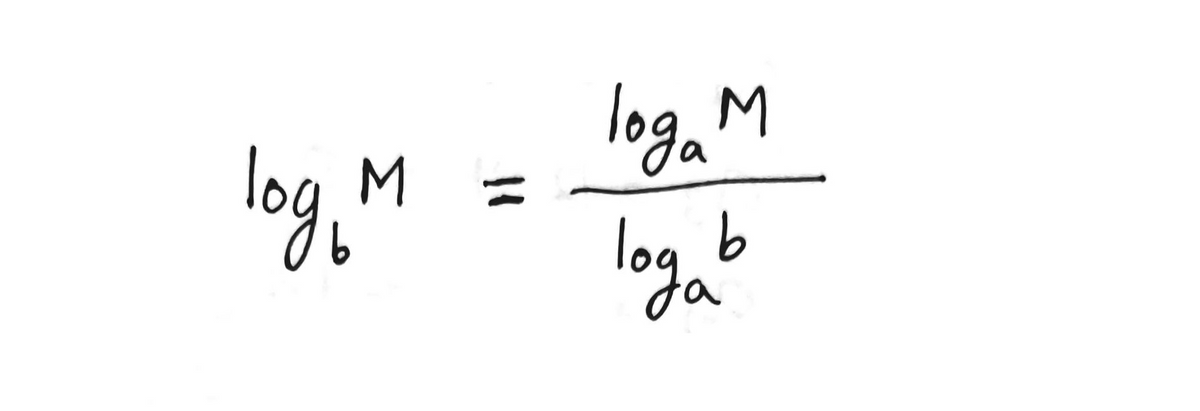
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

