Answered: (b) Test for a significant relationship…

MATLAB: An Introduction with Applications

6th Edition

ISBN:9781119256830

Author:Amos Gilat

Publisher:Amos Gilat

Chapter1: Starting With Matlab

Section: Chapter Questions

Problem 1P

See similar textbooks

Related questions

Question

### Statistical Analysis Using F Test

#### (b) Test for a Significant Relationship Using the F Test (α = 0.05)

**Null and Alternative Hypotheses:**

- $ H_0: \, \beta_1 = 0 $
- $ H_a: \, \beta_1 \neq 0 $ (This hypothesis is selected)

**Test Statistic:**

- The calculated test statistic value is **2.79**.

**p-value:**

- The calculated p-value is **0.049**.

**Conclusion:**

- **Reject $ H_0 $**: We conclude that the relationship between price ($) and overall score is significant.

#### (c) ANOVA Table

This section presents the ANOVA (Analysis of Variance) table summarizing the variance analysis for the data.

| Source of Variation | Sum of Squares | Degrees of Freedom | Mean Square | F | p-value |
|---------------------|----------------|-------------------|-------------|---------|------------|
| Regression | 1537.93 | 1 | 1537.93 | 20.78 | 0.010 |
| Error | 296.07 | 4 | 74.02 | | |
| Total | 1834 | 5 | | | |

- The F-value is **20.78** with a p-value of **0.010** which supports rejecting the null hypothesis, indicating a significant relationship between the variables.

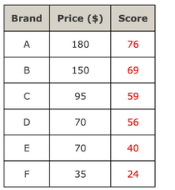
$### Analysis of Stereo Headphone Prices and Overall Scores #### Data Table The table below shows the price ($) and overall score for six stereo headphones tested by a magazine. The overall score considers sound quality and noise reduction on a scale from 0 (lowest) to 100 (highest). | Brand | Price ($) | Score | |-------|-----------|-------| | A | 180 | 76 | | B | 150 | 69 | | C | 95 | 59 | | D | 70 | 56 | | E | 40 | 40 | | F | 35 | 24 | #### Regression Analysis **Estimated Regression Equation:** \[ \hat{y} = 21.926421 + 0.320736x \] Where $x$ is the price in dollars, and $y$ is the overall score. The regression equation suggests that as the price of headphones increases, the overall score tends to increase. #### Hypothesis Testing We are using a significance level ($\alpha$) of 0.05 to test if there is a significant relationship between price and overall score. **Null and Alternative Hypotheses:** We are testing: - $H_0: \beta_1 = 0$ (No relationship between price and score) - $H_a: \beta_1 \neq 0$ (There is a relationship between price and score) From the options provided, the correct hypothesis set selected indicates: - $H_0: \beta_1 = 0$ - $H_a: \beta_1 \neq 0$ **Test Statistic and p-value:** - **Test Statistic:** 4.558263 - **p-value:** 0.010352 #### Conclusion Based on the p-value: - **Reject $H_0$:** Since the p-value (0.010352) is less than the significance level (0.05), we reject the null hypothesis. - **Conclusion:** There is a statistically significant relationship between the price of headphones and their overall score. This analysis indicates that as the price increases, there tends to be an improvement in the overall quality as measured by the score.$

Transcribed Image Text:### Analysis of Stereo Headphone Prices and Overall Scores #### Data Table The table below shows the price ($) and overall score for six stereo headphones tested by a magazine. The overall score considers sound quality and noise reduction on a scale from 0 (lowest) to 100 (highest). | Brand | Price ($) | Score | |-------|-----------|-------| | A | 180 | 76 | | B | 150 | 69 | | C | 95 | 59 | | D | 70 | 56 | | E | 40 | 40 | | F | 35 | 24 | #### Regression Analysis **Estimated Regression Equation:** \[ \hat{y} = 21.926421 + 0.320736x \] Where $x$ is the price in dollars, and $y$ is the overall score. The regression equation suggests that as the price of headphones increases, the overall score tends to increase. #### Hypothesis Testing We are using a significance level ($\alpha$) of 0.05 to test if there is a significant relationship between price and overall score. **Null and Alternative Hypotheses:** We are testing: - $H_0: \beta_1 = 0$ (No relationship between price and score) - $H_a: \beta_1 \neq 0$ (There is a relationship between price and score) From the options provided, the correct hypothesis set selected indicates: - $H_0: \beta_1 = 0$ - $H_a: \beta_1 \neq 0$ **Test Statistic and p-value:** - **Test Statistic:** 4.558263 - **p-value:** 0.010352 #### Conclusion Based on the p-value: - **Reject $H_0$:** Since the p-value (0.010352) is less than the significance level (0.05), we reject the null hypothesis. - **Conclusion:** There is a statistically significant relationship between the price of headphones and their overall score. This analysis indicates that as the price increases, there tends to be an improvement in the overall quality as measured by the score.

Expert Solution