Homework Help is Here – Start Your Trial Now!
Math
Advanced Math
b) Prove that 3abc ≤ a³ + b³ + c³ for nonnegative a, b, c. (Hint: In the in- equality of part (a), set w equal to the cube root of xyz.)

b) Prove that 3abc ≤ a³ + b³ + c³ for nonnegative a, b, c. (Hint: In the in- equality of part (a), set w equal to the cube root of xyz.)

Advanced Engineering Mathematics
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
See similar textbooks
icon
Related questions
Question
Please do part B only.
1.31. (+) Extensions of the AGM Inequality. a) Prove that 4xyzw ≤ x² + y² + 24 + w for real numbers x, y, z, w. (Hint: Use the inequality 2tu ²+u² repeatedly.) b) Prove that 3abc ≤ a³ + b³ + c³ for nonnegative a, b, c. (Hint: In the in- equality of part (a), set w equal to the cube root of xyz.) 1:32 (1) Assuming only arithmetic (not the quadratic formula or calculus) prove
Transcribed Image Text:1.31. (+) Extensions of the AGM Inequality. a) Prove that 4xyzw ≤ x² + y² + 24 + w for real numbers x, y, z, w. (Hint: Use the inequality 2tu ²+u² repeatedly.) b) Prove that 3abc ≤ a³ + b³ + c³ for nonnegative a, b, c. (Hint: In the in- equality of part (a), set w equal to the cube root of xyz.) 1:32 (1) Assuming only arithmetic (not the quadratic formula or calculus) prove
Expert Solution
Step 1

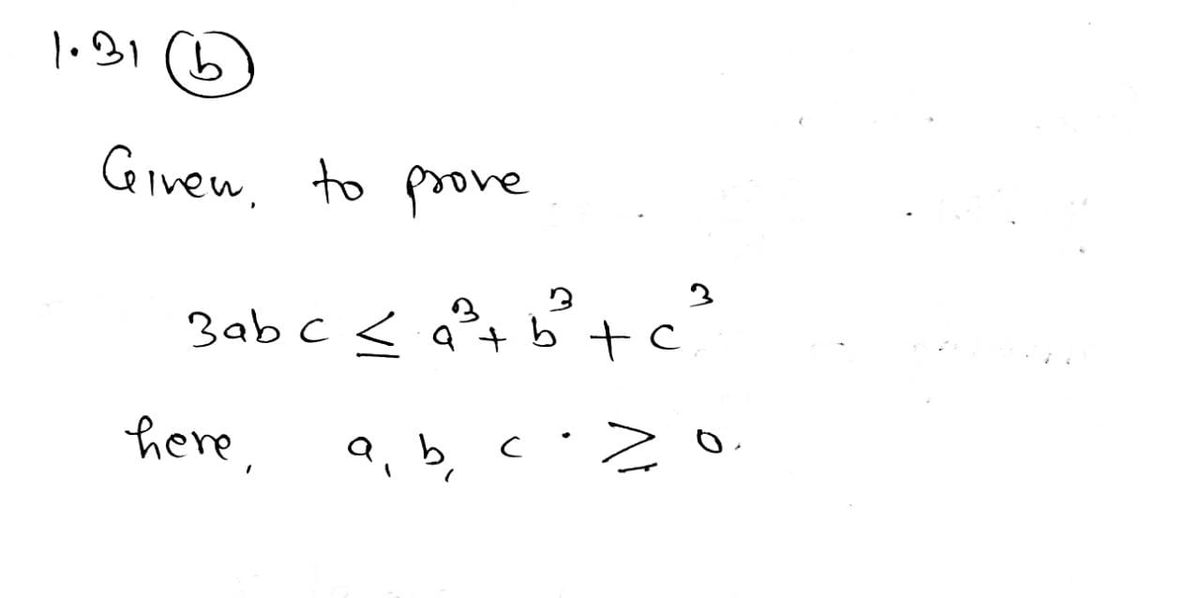
Advanced Math homework question answer, step 1, image 1

steps

Step by step

Solved in 2 steps with 2 images

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer
Recommended textbooks for you
Advanced Engineering Mathematics
Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education
Introductory Mathematics for Engineering Applicat…
Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY
Mathematics For Machine Technology
Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,
Basic Technical Mathematics
Basic Technical Mathematics
Advanced Math
ISBN:
9780134437705
Author:
Washington
Publisher:
PEARSON
Topology
Topology
Advanced Math
ISBN:
9780134689517
Author:
Munkres, James R.
Publisher:
Pearson,
SEE MORE TEXTBOOKS