Assuming there are n= 50,000 couples in the los ángeles area, what is the probability that more than one of them has the characteristics listed in the table? P( X > 1) =
Contingency Table
A contingency table can be defined as the visual representation of the relationship between two or more categorical variables that can be evaluated and registered. It is a categorical version of the scatterplot, which is used to investigate the linear relationship between two variables. A contingency table is indeed a type of frequency distribution table that displays two variables at the same time.
Binomial Distribution
Binomial is an algebraic expression of the sum or the difference of two terms. Before knowing about binomial distribution, we must know about the binomial theorem.
Assuming there are n= 50,000 couples in the los ángeles area, what is the
P( X > 1) =
![(c) Now let \( n \) represent the number of couples in the Los Angeles area who could have committed the crime. Let \( p \) represent the probability that a randomly selected couple has all 6 characteristics listed in the table. Assuming that the random variable \( X \) follows the binomial probability function, we have:
\[
P(X) = C(n,x) \cdot p^x \cdot (1-p)^{n-x}, \, x = 0, 1, 2, \ldots, n
\]
**Note:** Use the calculator link [http://stattrek.com/online-calculator/binomial.aspx](http://stattrek.com/online-calculator/binomial.aspx)
Assuming there are \( n = 50,000 \) couples in the Los Angeles area, what is the probability that more than one of them has the characteristics listed in the table?
\[
P(X > 1) =
\]
**Explanation:**
The problem describes a binomial probability scenario where you're given the total number of trials (\( n = 50,000 \)) and the probability of a single success (\( p \)), and we're asked to find the probability of more than one success (\( X > 1 \)). The provided formula helps to compute the probability for various values of \( X \), while the calculator link is a tool for solving such a complex probability calculation.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F0fbc9864-00b0-4b62-b8b1-d92e884a9479%2F7a5c4327-fa1f-40f5-84f3-6bca59c1e840%2Flr2mwu7_processed.jpeg&w=3840&q=75)
Obtain the probability that more than one of the 50,000 couples has all the listed characteristics:
Here, n = 50,000 and p = 0.0000000833.
Denote the number of couples who have all the listed characteristics as X.
Here, X ~ B(50,000, 0.0000000833).
The probability that more than one of the 50,000 couples has all the characteristics is obtained as 0.0000086 from the calculation given below:
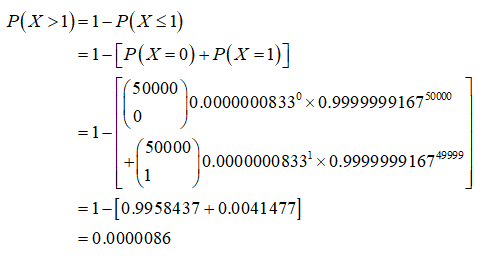
Step by step
Solved in 2 steps with 1 images









