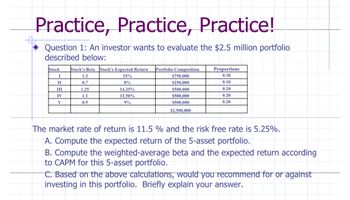
Assume you have invested in two other stocks: Stock A has a beta of 1.20 and Stock B has a beta of 0.8. Rf= 2% and Rm = 12%. Using CAPM, what are the expected returns for each stock? Return of stock = Risk free rate + beta ( market rate of return - risk free rate of return) Return of Stock A = 2% + 1.20 (12% - 2%) = 2.12% Return of Stock B = 2% + 0.80 (12% - 2%) = 2.08% What is the expected return of an equally weighted portfolio of these two stocks? Weight of stock A = 0.50 Weight of Stock B = 0.50 Expected return = (Return of Stock A * weight of Stock A) + (Return of Stock B * weight of stock B) = (2.12 * 0.50) + (2.08*0.50) = 1.06 + 1.04 = 3% What is the beta of an equally weighted portfolio of these two stocks? Beta of portfolio = (Beta of Stock A * weight of stock A) + (Beta of Stock B * weight of Stock B) = (1.20*0.50) + (0.80*0.50) = 0.60 + 0.40 = 1 Beta of portfolio = 1 (iv) Sketch the SML to represent the market’s expected return (Please do this one) (v) Place Stock A and B on the SML and state if they are over- valued or Under-valued. (Please do this one)
Assume you have invested in two other stocks: Stock A has a beta of 1.20 and Stock B has a beta of 0.8. Rf= 2% and Rm = 12%. Using CAPM, what are the expected returns for each stock? Return of stock = Risk free rate + beta ( market rate of return - risk free rate of return) Return of Stock A = 2% + 1.20 (12% - 2%) = 2.12% Return of Stock B = 2% + 0.80 (12% - 2%) = 2.08% What is the expected return of an equally weighted portfolio of these two stocks? Weight of stock A = 0.50 Weight of Stock B = 0.50 Expected return = (Return of Stock A * weight of Stock A) + (Return of Stock B * weight of stock B) = (2.12 * 0.50) + (2.08*0.50) = 1.06 + 1.04 = 3% What is the beta of an equally weighted portfolio of these two stocks? Beta of portfolio = (Beta of Stock A * weight of stock A) + (Beta of Stock B * weight of Stock B) = (1.20*0.50) + (0.80*0.50) = 0.60 + 0.40 = 1 Beta of portfolio = 1 (iv) Sketch the SML to represent the market’s expected return (Please do this one) (v) Place Stock A and B on the SML and state if they are over- valued or Under-valued. (Please do this one)
Essentials Of Investments
11th Edition
ISBN:9781260013924
Author:Bodie, Zvi, Kane, Alex, MARCUS, Alan J.
Publisher:Bodie, Zvi, Kane, Alex, MARCUS, Alan J.
Chapter1: Investments: Background And Issues
Section: Chapter Questions
Problem 1PS
Related questions
Question
- Assume you have invested in two other stocks: Stock A has a beta of 1.20 and Stock B has a beta of 0.8. Rf= 2% and Rm = 12%.
- Using
CAPM , what are the expected returns for each stock?
Return of stock = Risk free rate + beta ( market
Return of Stock A = 2% + 1.20 (12% - 2%) = 2.12%
Return of Stock B = 2% + 0.80 (12% - 2%) = 2.08%
- What is the expected return of an equally weighted portfolio of these two stocks?
Weight of stock A = 0.50
Weight of Stock B = 0.50
Expected return = (Return of Stock A * weight of Stock A) + (Return of Stock B * weight of stock B)
= (2.12 * 0.50) + (2.08*0.50)
= 1.06 + 1.04 = 3%
- What is the beta of an equally weighted portfolio of these two stocks?
Beta of portfolio = (Beta of Stock A * weight of stock A) + (Beta of Stock B * weight of Stock B)
= (1.20*0.50) + (0.80*0.50)
= 0.60 + 0.40 = 1
Beta of portfolio = 1
(iv) Sketch the SML to represent the market’s expected return (Please do this one)
(v) Place Stock A and B on the SML and state if they are over- valued or Under-valued. (Please do this one)
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 4 steps with 1 images
Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
Transcribed Image Text:Practice, Practice, Practice!
Question 1: An investor wants to evaluate the $2.5 million portfolio
described below:
Stock
I
II
III
IV
V
Stock's Beta Stock's Expected Return Portfolio Composition
15%
8%
16.25%
12.50%
9%
1.3
0.7
1.25
1.1
0.9
$750,000
$250,000
$500,000
$500,000
$500,000
$2,500,000
Proportions
0.30
0.10
0.20
0.20
0.20
The market rate of return is 11.5 % and the risk free rate is 5.25%.
A. Compute the expected return of the 5-asset portfolio.
B. Compute the weighted-average beta and the expected return according
to CAPM for this 5-asset portfolio.
C. Based on the above calculations, would you recommend for or against
investing in this portfolio. Briefly explain your answer.
Solution
by Bartleby ExpertKnowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, finance and related others by exploring similar questions and additional content below.Recommended textbooks for you
Essentials Of Investments
Finance
ISBN:
9781260013924
Author:
Bodie, Zvi, Kane, Alex, MARCUS, Alan J.
Publisher:
Mcgraw-hill Education,
Essentials Of Investments
Finance
ISBN:
9781260013924
Author:
Bodie, Zvi, Kane, Alex, MARCUS, Alan J.
Publisher:
Mcgraw-hill Education,
Foundations Of Finance
Finance
ISBN:
9780134897264
Author:
KEOWN, Arthur J., Martin, John D., PETTY, J. William
Publisher:
Pearson,
Fundamentals of Financial Management (MindTap Cou…
Finance
ISBN:
9781337395250
Author:
Eugene F. Brigham, Joel F. Houston
Publisher:
Cengage Learning
Corporate Finance (The Mcgraw-hill/Irwin Series i…
Finance
ISBN:
9780077861759
Author:
Stephen A. Ross Franco Modigliani Professor of Financial Economics Professor, Randolph W Westerfield Robert R. Dockson Deans Chair in Bus. Admin., Jeffrey Jaffe, Bradford D Jordan Professor
Publisher:
McGraw-Hill Education