Assume that the |+z) and |-z) states for an electron in a magnetic field are energy eigen- vectors with energies E and 0, respectively, and assume that the electron's state at t = 0 is -M Find the probability that we will determine this electron's spin to be in the +x direction at time t |y(0))
Assume that the |+z) and |-z) states for an electron in a magnetic field are energy eigen- vectors with energies E and 0, respectively, and assume that the electron's state at t = 0 is -M Find the probability that we will determine this electron's spin to be in the +x direction at time t |y(0))
Related questions
Question
please help thnk you
![Assume that the \(|+z\rangle\) and \(|-z\rangle\) states for an electron in a magnetic field are energy eigenvectors with energies \(E\) and \(0\), respectively, and assume that the electron’s state at \(t = 0\) is
\[
|\psi(0)\rangle = \begin{bmatrix} \sqrt{\frac{4}{5}} \\ \sqrt{\frac{1}{5}} \end{bmatrix}
\]
Find the probability that we will determine this electron’s spin to be in the \(+x\) direction at time \(t\).](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F5b55a0fb-5dff-4587-97c0-c3ec381e9c7e%2F7e71a0db-c650-4167-a99a-cdf639c05eb7%2Fl5rtcqd_processed.png&w=3840&q=75)
Transcribed Image Text:Assume that the \(|+z\rangle\) and \(|-z\rangle\) states for an electron in a magnetic field are energy eigenvectors with energies \(E\) and \(0\), respectively, and assume that the electron’s state at \(t = 0\) is
\[
|\psi(0)\rangle = \begin{bmatrix} \sqrt{\frac{4}{5}} \\ \sqrt{\frac{1}{5}} \end{bmatrix}
\]
Find the probability that we will determine this electron’s spin to be in the \(+x\) direction at time \(t\).
Expert Solution
Step 1: Given data
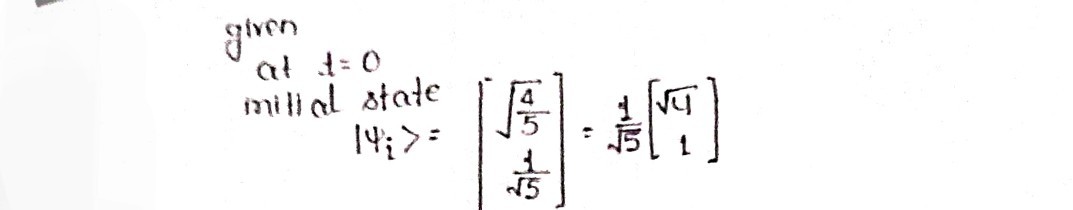
Step by step
Solved in 3 steps with 2 images
