Assume that fk and gm are related by the above equations parts (a) and (b) below. (a) Show that N-I - IMP Σ Clfkl², k=0 N-1 Σ19m² = m=0 which is a version of Parseval's Theorem for the DFT. (b) If fk = fk-n, where n is any integer, show that the DFT of f is given by 9m = exp(2πi nm/N)gm- Note that if the index of fk, fk, 9m, or gm is outside of the range 0, 1, 2, ..., N- 1 it is understood to be brought back into this range by adding or sub- tracting the necessary integer multiple of N (equivalent to assuming they are periodic with a period of N). This result shows that shifting fe by a constant offset multiplies gm by a linearly-varying phase.
Assume that fk and gm are related by the above equations parts (a) and (b) below. (a) Show that N-I - IMP Σ Clfkl², k=0 N-1 Σ19m² = m=0 which is a version of Parseval's Theorem for the DFT. (b) If fk = fk-n, where n is any integer, show that the DFT of f is given by 9m = exp(2πi nm/N)gm- Note that if the index of fk, fk, 9m, or gm is outside of the range 0, 1, 2, ..., N- 1 it is understood to be brought back into this range by adding or sub- tracting the necessary integer multiple of N (equivalent to assuming they are periodic with a period of N). This result shows that shifting fe by a constant offset multiplies gm by a linearly-varying phase.
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
Question 6?
![### The Discrete Fourier Transform (DFT)
#### Definition:
The Discrete Fourier Transform (DFT) is defined for a discrete set of equally spaced values as follows:
\[
g_m = \frac{1}{\sqrt{N}} \sum_{k=0}^{N-1} f_k \exp(2\pi i km/N) \quad m = 0, 1, 2, \ldots, N-1
\]
where the function \( f(x) \) is used only for discrete equally-spaced \( x \) values:
\[
f_k = f(x_k)
\]
\[
x_k = \frac{2\pi k}{N} \quad k = 0, 1, 2, \ldots, N-1
\]
#### Orthogonality Relation:
In class, an orthogonality relation was derived:
\[
\sum_{k=0}^{N-1} \exp(-2\pi i kn/N) \exp(2\pi i kn/N) = N \delta_{m,n}
\]
by recognizing that the sum is a geometric series. Note that \( n = 0, 1, 2, \ldots, N-1 \) as well.
#### Inverse Transform:
The inverse transform is determined by:
\[
f_k = \frac{1}{\sqrt{N}} \sum_{m=0}^{N-1} g_m \exp(-2\pi i mk/N) \quad m = 0, 1, 2, \ldots, N-1
\]
#### Relations and Theorems:
Assume that \( f_k \) and \( g_m \) are related by the equations derived above. Then:
**(a)** Show that:
\[
\sum_{m=0}^{N-1} |g_m|^2 = \sum_{k=0}^{N-1} |f_k|^2
\]
which is a version of Parseval's Theorem for the DFT.
**(b)** If \( \tilde{f}_k = f_{k-n} \), where \( n \) is any integer, show that the DFT of \( \tilde{f}_k \) is given by:
\[
\tilde{g}_m = \exp(2\pi i nm](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F9b65ef36-cf51-4f81-80a6-74e205c9e9b1%2F110fcf66-f329-4d13-b39f-f67552f73829%2Fql6bv5k_processed.jpeg&w=3840&q=75)
Transcribed Image Text:### The Discrete Fourier Transform (DFT)
#### Definition:
The Discrete Fourier Transform (DFT) is defined for a discrete set of equally spaced values as follows:
\[
g_m = \frac{1}{\sqrt{N}} \sum_{k=0}^{N-1} f_k \exp(2\pi i km/N) \quad m = 0, 1, 2, \ldots, N-1
\]
where the function \( f(x) \) is used only for discrete equally-spaced \( x \) values:
\[
f_k = f(x_k)
\]
\[
x_k = \frac{2\pi k}{N} \quad k = 0, 1, 2, \ldots, N-1
\]
#### Orthogonality Relation:
In class, an orthogonality relation was derived:
\[
\sum_{k=0}^{N-1} \exp(-2\pi i kn/N) \exp(2\pi i kn/N) = N \delta_{m,n}
\]
by recognizing that the sum is a geometric series. Note that \( n = 0, 1, 2, \ldots, N-1 \) as well.
#### Inverse Transform:
The inverse transform is determined by:
\[
f_k = \frac{1}{\sqrt{N}} \sum_{m=0}^{N-1} g_m \exp(-2\pi i mk/N) \quad m = 0, 1, 2, \ldots, N-1
\]
#### Relations and Theorems:
Assume that \( f_k \) and \( g_m \) are related by the equations derived above. Then:
**(a)** Show that:
\[
\sum_{m=0}^{N-1} |g_m|^2 = \sum_{k=0}^{N-1} |f_k|^2
\]
which is a version of Parseval's Theorem for the DFT.
**(b)** If \( \tilde{f}_k = f_{k-n} \), where \( n \) is any integer, show that the DFT of \( \tilde{f}_k \) is given by:
\[
\tilde{g}_m = \exp(2\pi i nm
Expert Solution
Step 1: Part a
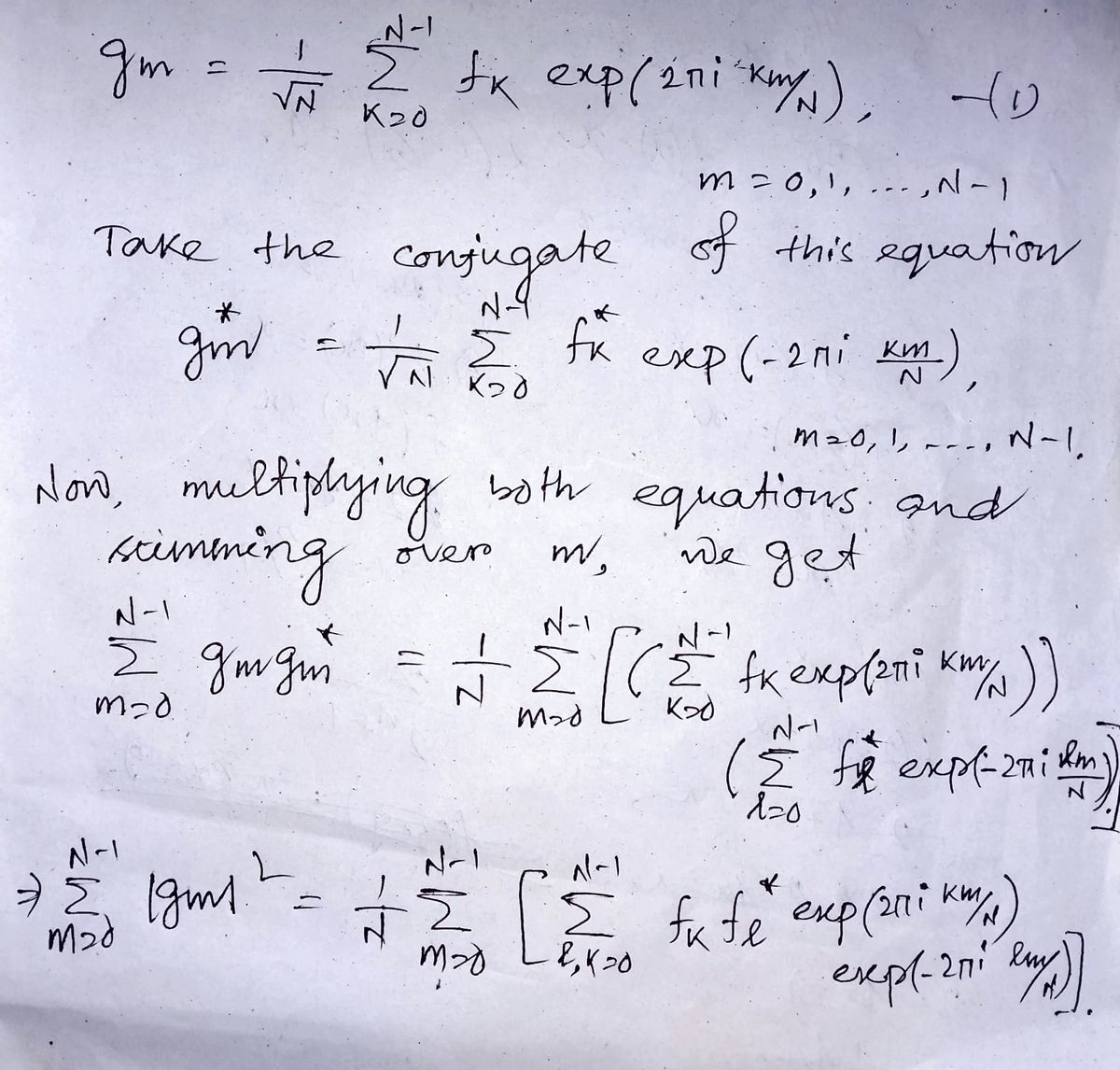
Step by step
Solved in 4 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

