Assume t = 0.005 a.) Write a sinusoidal function V(t) to model the b.) Use your function to determine the voltage a- It is in seconds. One city averages 14 hours of daylight in June, and 12 both in March and in September. Assume is one year and let t = 1 represent January. Write a sinusoidal function H(t) to model he Use your function to predict the hours of d month of November. a.) b.) 6. The top of a building designed by Gractals Inco 10 meters and then right 10 meters of its stable ec One full swing from equilibrium to the left, to th
Assume t = 0.005 a.) Write a sinusoidal function V(t) to model the b.) Use your function to determine the voltage a- It is in seconds. One city averages 14 hours of daylight in June, and 12 both in March and in September. Assume is one year and let t = 1 represent January. Write a sinusoidal function H(t) to model he Use your function to predict the hours of d month of November. a.) b.) 6. The top of a building designed by Gractals Inco 10 meters and then right 10 meters of its stable ec One full swing from equilibrium to the left, to th
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
#6
![5.
a.)
Assume voltage is at its maximum when time
range is [-170, +170] volts.
a.)
The electricity in a U.S. house is called alternating current (C)
sume that the frequency is 60 cycles/second and that the voltage
use the voltage and current vary sinusoidally with time.
t = 0.005556 second.
Write a sinusoidal function V (t) to model that voltage, where
t = 0.008 sec.
t is in seconds.
Use your function to determine the voltage at
b.)
One city averages 14 hours of daylight in June, 10 in December,
Assume that the period
and 12 both in March and in September.
is one year and let t = 1 represent January.
Write a sinusoidal function H(t) to model hours of daylight.
Use your function to predict the hours of daylight for the
month of November.
a.)
b.)
6.
The top of a building designed by Gractals Incorporated sways left
10 meters and then right 10 meters of its stable equilibrium position.
One full swing from equilibrium to the left, to the right and then
back to equilibrium takes 4 seconds. At t = 1 sec. the building is
at equilibrium and about to swing left again.
a.) Write a sinusoidal function D (t) to model that building top's
displacement.
b.)
What is the displacement of the top of the building
at 3.5 seconds?
The number of visible sun spots varies rhythmically from 10
to 110 per year over a period of eleven years.
occurred in the year 2014.
The 110 max last
Write](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F2816e768-d46c-42f8-b287-986238abcd2a%2F42b56be5-23fc-4a63-a29c-7ed006571a84%2F88e1urt_processed.jpeg&w=3840&q=75)
Transcribed Image Text:5.
a.)
Assume voltage is at its maximum when time
range is [-170, +170] volts.
a.)
The electricity in a U.S. house is called alternating current (C)
sume that the frequency is 60 cycles/second and that the voltage
use the voltage and current vary sinusoidally with time.
t = 0.005556 second.
Write a sinusoidal function V (t) to model that voltage, where
t = 0.008 sec.
t is in seconds.
Use your function to determine the voltage at
b.)
One city averages 14 hours of daylight in June, 10 in December,
Assume that the period
and 12 both in March and in September.
is one year and let t = 1 represent January.
Write a sinusoidal function H(t) to model hours of daylight.
Use your function to predict the hours of daylight for the
month of November.
a.)
b.)
6.
The top of a building designed by Gractals Incorporated sways left
10 meters and then right 10 meters of its stable equilibrium position.
One full swing from equilibrium to the left, to the right and then
back to equilibrium takes 4 seconds. At t = 1 sec. the building is
at equilibrium and about to swing left again.
a.) Write a sinusoidal function D (t) to model that building top's
displacement.
b.)
What is the displacement of the top of the building
at 3.5 seconds?
The number of visible sun spots varies rhythmically from 10
to 110 per year over a period of eleven years.
occurred in the year 2014.
The 110 max last
Write
Expert Solution
Step 1
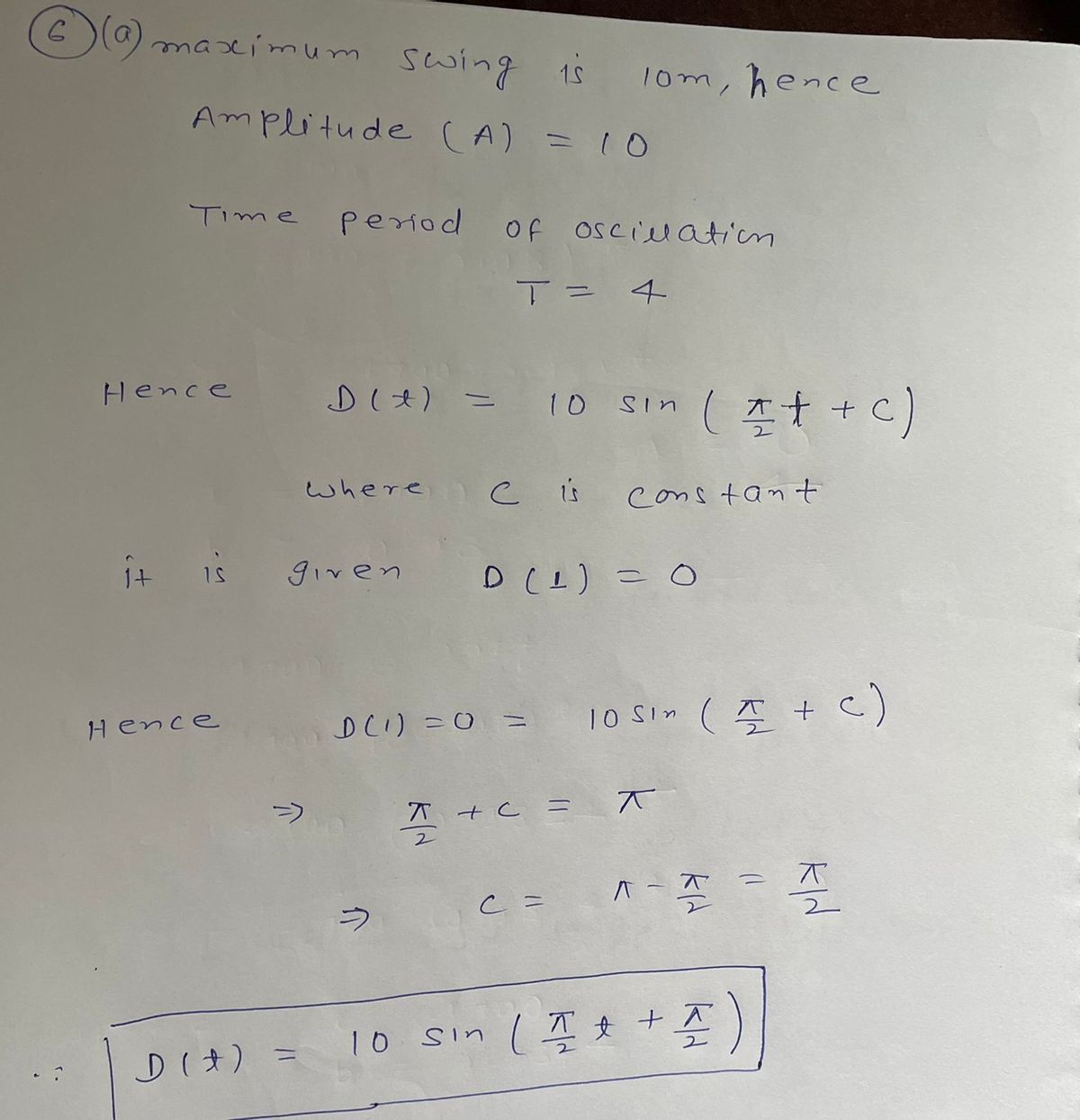
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

