As in Example 1c of Section 5.1, assume tan e = -2.7, and e is in the second quadrant. Use one of the fundamental identities to find cot(-0). Provide 4 decimal places. Answer:
As in Example 1c of Section 5.1, assume tan e = -2.7, and e is in the second quadrant. Use one of the fundamental identities to find cot(-0). Provide 4 decimal places. Answer:
Trigonometry (11th Edition)
11th Edition
ISBN:9780134217437
Author:Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher:Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Chapter1: Trigonometric Functions
Section: Chapter Questions
Problem 1RE:
1. Give the measures of the complement and the supplement of an angle measuring 35°.
Related questions
Question
The second image is Example 1.c. For reference

Transcribed Image Text:As in Example 1c of Section 5.1, assume \(\tan \theta = -2.7\), and \(\theta\) is in the second quadrant. Use one of the fundamental identities to find \(\cot(-\theta)\). Provide 4 decimal places.
**Answer:**
![The image contains a trigonometry exercise involving the manipulation of trigonometric identities. Below is a transcription with explanations:
### Trigonometric Identities and Calculations
- **Given:**
- \(\sin \theta = \frac{5 \sqrt{34}}{34}\)
- **Objective:**
- Use reciprocal identities to relate the tangent and cotangent functions.
#### Example Problem
- **Expression:**
\[
\cot(-\theta)
\]
- **Calculations:**
1. **Reciprocal Identity:**
\[
\cot(-\theta) = \frac{1}{\tan(-\theta)}
\]
2. **Even-Odd Identity:**
- \(\tan(-\theta) = -\tan(\theta)\)
3. **Substitute and Simplify:**
\[
= \frac{1}{-\tan(\theta)} = -\frac{1}{\tan(\theta)}
\]
4. **Further Simplification:**
\[
= -\left(\frac{1}{\frac{5}{3}}\right) = -\left(\frac{3}{5}\right)
\]
5. **Multiply and Rewrite:**
\[
= 1 \div \left(\frac{5}{3}\right) = 1 \cdot \frac{3}{5} = \frac{3}{5}
\]
#### Exercises
Now try solving these similar problems:
- **Exercises:**
- 11
- 19
- 31
This section demonstrates the application of reciprocal identities and even-odd identities associated with trigonometric functions to solve expressions involving cotangents and tangents. It is important to thoroughly understand these identities to simplify and solve trigonometric problems effectively.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F26a21d52-7816-4917-a16a-44de3883c3a3%2Fd8b45f53-d7cd-4ddc-89d1-2342c02bbf6b%2F82hpzgm_processed.jpeg&w=3840&q=75)
Transcribed Image Text:The image contains a trigonometry exercise involving the manipulation of trigonometric identities. Below is a transcription with explanations:
### Trigonometric Identities and Calculations
- **Given:**
- \(\sin \theta = \frac{5 \sqrt{34}}{34}\)
- **Objective:**
- Use reciprocal identities to relate the tangent and cotangent functions.
#### Example Problem
- **Expression:**
\[
\cot(-\theta)
\]
- **Calculations:**
1. **Reciprocal Identity:**
\[
\cot(-\theta) = \frac{1}{\tan(-\theta)}
\]
2. **Even-Odd Identity:**
- \(\tan(-\theta) = -\tan(\theta)\)
3. **Substitute and Simplify:**
\[
= \frac{1}{-\tan(\theta)} = -\frac{1}{\tan(\theta)}
\]
4. **Further Simplification:**
\[
= -\left(\frac{1}{\frac{5}{3}}\right) = -\left(\frac{3}{5}\right)
\]
5. **Multiply and Rewrite:**
\[
= 1 \div \left(\frac{5}{3}\right) = 1 \cdot \frac{3}{5} = \frac{3}{5}
\]
#### Exercises
Now try solving these similar problems:
- **Exercises:**
- 11
- 19
- 31
This section demonstrates the application of reciprocal identities and even-odd identities associated with trigonometric functions to solve expressions involving cotangents and tangents. It is important to thoroughly understand these identities to simplify and solve trigonometric problems effectively.
Expert Solution
Step 1
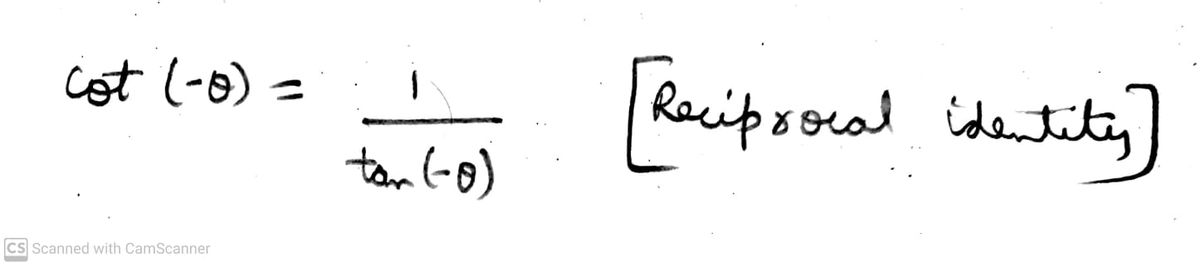
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Trigonometry (11th Edition)
Trigonometry
ISBN:
9780134217437
Author:
Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher:
PEARSON

Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781305652224
Author:
Charles P. McKeague, Mark D. Turner
Publisher:
Cengage Learning


Trigonometry (11th Edition)
Trigonometry
ISBN:
9780134217437
Author:
Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher:
PEARSON

Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781305652224
Author:
Charles P. McKeague, Mark D. Turner
Publisher:
Cengage Learning


Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781337278461
Author:
Ron Larson
Publisher:
Cengage Learning