Area Under the Standard Normal Curve A 0.00 0.000 0.56 0.212 1.12 0.369 1.68 0.454 2.24 0.487 2.80 0.497 0.01 0.004 0.57 0.216 1.13 0.371 1.69 0.454 2.25 0.488 2.81 0.498 0.02 0.008 0.58 0.219 1.14 0.373 1.70 0.455 2.26 0.488 2.82 0.498 0.03 0.012 0.59 0.222 1.15 0.375 1.71 0.456 2.27 0.488 2.83 0.498 0.04 0.016 0.60 0.226 1.16 0.377 1.72 0.457 2.28 0.489 2.84 0.498 0.458 0.459 0.05 0.020 0.61 0.229 1.17 0.379 1.73 2.29 0.489 2.85 0.498 0.06 0.024 0.62 0.232 1.18 0.381 1.74 2.30 0.489 2.86 0.498 0.07 0.028 0.63 0.236 1.19 0.383 1.75 0.460 2.31 0.490 2.87 0.498 0.08 0.032 0.64 0.239 1.20 0.385 1.76 0.461 2.32 0.490 2.88 0.498 0.09 0.036 0.65 0.242 1.21 0.387 1.77 0.462 2.33 0.490 2.89 0.498 0.10 0.040 0.66 0.245 1.22 0.389 1.78 0.462 2.34 0.490 2.90 0.498 0.11 0.044 0.67 0.249 1.23 0.391 1.79 0.463 2.35 0.491 2.91 0.498 0.12 0.048 0.68 0.252 1.24 0.393 1.80 0.464 2.36 0.491 2.92 0.498 0.13 0.052 0.69 0.255 1.25 0,394 1.81 0.465 2.37 0.491 2.93 0.498 0.14 0.056 0.70 0.258 1.26 0.396 1.82 0.466 2.38 0.491 2.94 0.498 0.060 0.398 0.466 2.39 2.95 0.492 0.492 0.15 0.71 0.261 1.27 1.83 0.498 0.16 0.064 0.72 0.264 1.28 0.400 1.84 0.467 2.40 2.96 0.498 0.17 0.067 0.73 0.267 1.29 0.401 1.85 0.468 2.41 0.492 2.97 0.499 0.18 0.071 0.74 0.270 1.30 0.403 1.86 0.469 2.42 0.492 2.98 0.499 0.19 0.075 0.75 0.273 1.31 0.405 1.87 0.469 2.43 0.492 2.99 0.499 0.20 0.079 0.76 0.276 1.32 0.407 1.88 0.470 2.44 0.493 3.00 0.499 0.21 0.083 0.77 0.279 1.33 0.408 1.89 0.471 2.45 0.493 3.01 0.499 0.22 0.087 0.78 0.282 1.34 0.410 1.90 0.471 2.46 0.493 3.02 0.499 0.23 0.091 0.79 0.285 1.35 0.411 1.91 0.472 2.47 0.493 3.03 0.499 0.24 0.095 0.80 0.288 1.36 0.413 1.92 0.473 2.48 0.493 3.04 0.499 0.25 0.415 0.099 0.103 0.81 0.291 1.37 1.93 0.473 2,49 0.494 3.05 0.499 0.26 0.82 0.294 1.38 0.416 1.94 0.474 2.50 0.494 3.06 0.499 0.27 0.106 0.83 0.297 1.39 0.418 1.95 0.474 2.51 0.494 3.07 0.499 0.499 0.499 0.28 0.110 0.84 0.300 1.40 0.419 1.96 0.475 2.52 0.494 3.08 0.29 0.114 0.85 0.302 1.41 0.421 1.97 0.476 2.53 0.494 3.09 0.118 0.122 0.30 0.86 0.305 1.42 0.422 1.98 0.476 2.54 0.494 3.10 0.499 0.495 0.495 0.31 0.87 0.308 1.43 0.424 1.99 0.477 2.55 3.11 0.499 0.32 0.126 0.88 0.311 1.44 0.425 2.00 0.477 2.56 3.12 0.499 0,33 0.129 0.89 0.313 1.45 0.426 2.01 0.478 2.57 0.495 3.13 0.499 0.495 0.495 0.34 0.133 0.90 0.316 1.46 0.428 2.02 0.478 2.58 3.14 0.499 0.35 0.137 0.91 0.319 1.47 0.429 2.03 0.479 2.59 3.15 0.499 0.36 0.141 0.92 0.321 1.48 0.431 2.04 0.479 2.60 0.495 3.16 0.499 0.37 0.144 0.93 0.324 1.49 0.432 2.05 0.480 2.61 0.495 3.17 0.499 0.148 0.433 0.434 0.38 0.94 0.326 1.50 2.06 0.480 2.62 0.496 3.18 0.499 0.39 0.152 0.95 0.329 1.51 2.07 0.481 2.63 0.496 3.19 0.499 0.40 0.155 0.96 0.331 1.52 0.436 2.08 0.481 2.64 0.496 3.20 0.499 0.41 0.159 0.97 0.334 1.53 0.437 2.09 0.482 2.65 0.496 3.21 0.499 0.42 0.163 0.98 0.336 1.54 0.438 2.10 0.482 2.66 0.496 3.22 0.499 0.43 0.166 0.99 0.339 1.55 0.439 2.11 0.483 2.67 0.496 3.23 0.499 0.44 0.170 1.00 0.341 1.56 0.441 2.12 0.483 2.68 0.496 3.24 0.499 0.45 0.174 1.01 0.344 1.57 0.442 2.13 0.483 2.69 0.496 3.25 0.499 0.46 0.177 1.02 0.346 1.58 0.443 2.14 0.484 2.70 0.497 3.26 0.499 0.47 0.181 1.03 0.348 1.59 0.444 2.15 0.484 2.71 0.497 3.27 0.499 0.48 0.184 1.04 0.351 1.60 0.445 2.16 0.485 2.72 0.497 3.28 0.499 0.49 0.188 1.05 0.353 1.61 0.446 2.17 0.485 2.73 0.497 3.29 0.499 0,50 0.191 1.06 0.355 1.62 0.447 2.18 0.485 2.74 0.497 3.30 0.500 0.51 0.195 1.07 0.358 1.63 0.448 2.19 0.486 2.75 0.497 3.31 0.500 0.52 0.198 1.08 0.360 1.64 0.449 2.20 0.486 2.76 0.497 3.32 0.500 0.53 0.202 1.09 0.362 1.65 0.451 2.21 0.486 2.77 0.497 3.33 0.500 0.54 0.205 1.10 0.364 1.66 0.452 2.22 0.487 2.78 0.497 0.55 0.209 1.11 0.367 1.67 0.453 2.23 0.487 2.79 0.497
Continuous Probability Distributions
Probability distributions are of two types, which are continuous probability distributions and discrete probability distributions. A continuous probability distribution contains an infinite number of values. For example, if time is infinite: you could count from 0 to a trillion seconds, billion seconds, so on indefinitely. A discrete probability distribution consists of only a countable set of possible values.
Normal Distribution
Suppose we had to design a bathroom weighing scale, how would we decide what should be the range of the weighing machine? Would we take the highest recorded human weight in history and use that as the upper limit for our weighing scale? This may not be a great idea as the sensitivity of the scale would get reduced if the range is too large. At the same time, if we keep the upper limit too low, it may not be usable for a large percentage of the population!
The cholesterol levels of a group of young women at a university are
%
(b) between 189 and 221
%

From the provided information,
Mean (µ) = 187
Standard deviation (σ) = 35
Let X be a random variable which represents the cholesterol level of a young women at a university.
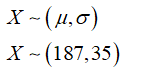
a)
The required percentage of the young women which have cholesterol levels greater than 224 can be obtained as: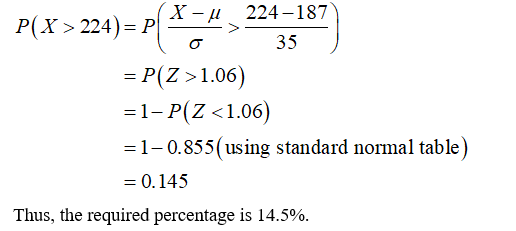
Step by step
Solved in 3 steps with 3 images









