Elementary Geometry For College Students, 7e
7th Edition
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Alexander, Daniel C.; Koeberlein, Geralyn M.
ChapterP: Preliminary Concepts
SectionP.CT: Test
Problem 1CT
Related questions
Question

Transcribed Image Text:### Transcription for Educational Use
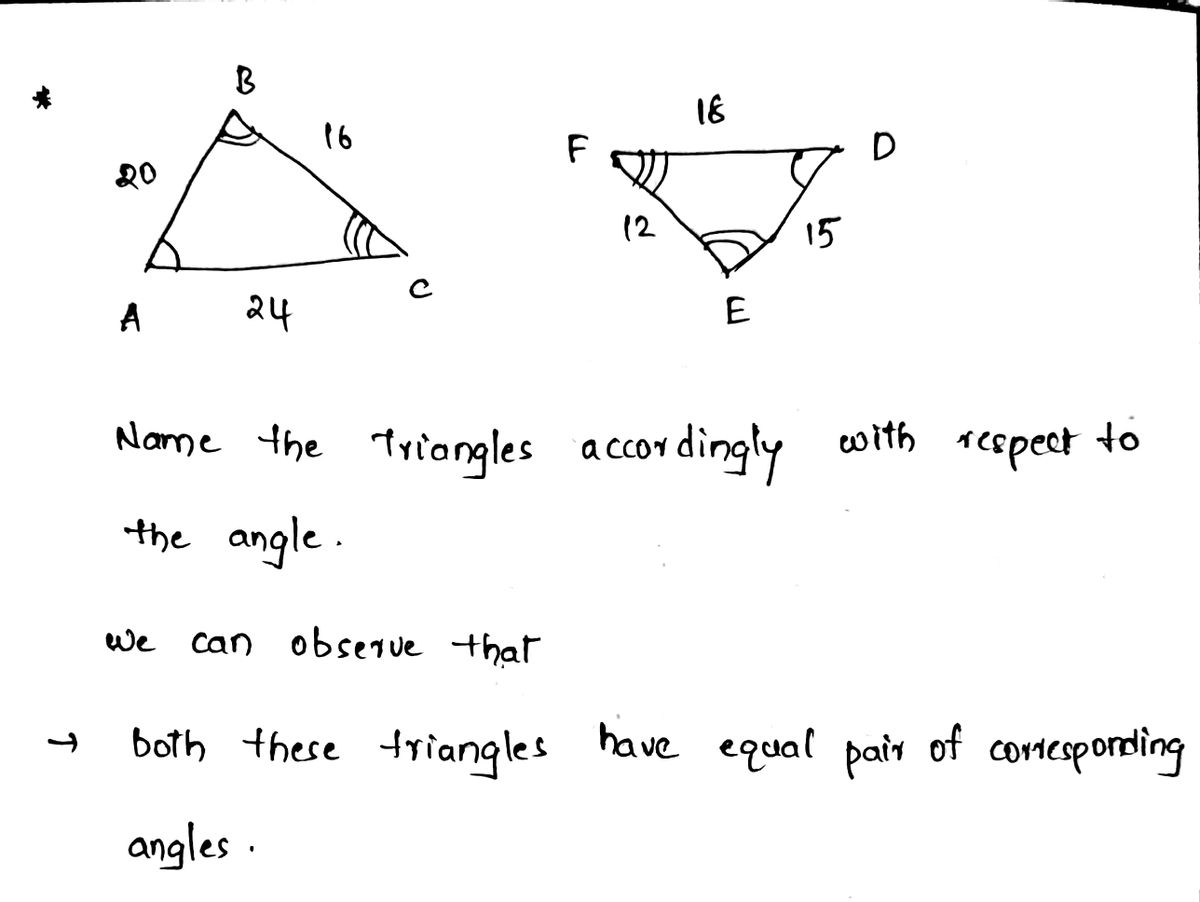
**Question:** Are the two triangles similar?
**Diagrams:**
- **First Triangle:**
- Sides: 20, 16, 24
- It shows angle markers indicating possible congruency with the second triangle.
- **Second Triangle:**
- Sides: 18, 12, 15
- It shows angle markers that correspond with those of the first triangle, indicating possible angle congruency.
**Your answer:**
- ○ Yes
- ○ No
### Explanation of Triangles
- **Similarity Criteria:**
- Two triangles are similar if their corresponding angles are equal and their corresponding sides are proportional.
- **Examining Side Ratios:**
- Compare the ratio of corresponding sides:
- \( \frac{20}{18} \), \( \frac{16}{12} \), \( \frac{24}{15} \)
- Check if these ratios are equivalent.
- **Conclusion:**
- If the ratios are equal, the triangles are similar. If not, they are not similar.
This activity requires understanding and applying the conditions for triangle similarity using side ratios and angle congruency.
Expert Solution
Step 1
Similar triangles are two or more triangles with the
- same shape,
- equal pair of corresponding angles, and
- same ratio of the corresponding sides
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Elementary Geometry For College Students, 7e
Geometry
ISBN:
9781337614085
Author:
Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:
Cengage,

Elementary Geometry for College Students
Geometry
ISBN:
9781285195698
Author:
Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:
Cengage Learning

Elementary Geometry For College Students, 7e
Geometry
ISBN:
9781337614085
Author:
Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:
Cengage,

Elementary Geometry for College Students
Geometry
ISBN:
9781285195698
Author:
Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:
Cengage Learning