Apply the BUC algorithm on the following table for minCount=4. You should describe the process and show all the cells (with measure values) that belong to the iceberg cube. A B C D count a1 b1 c1 d1 1 a1 b2 c1 d1 3 a2 b1 c1 d2 1 a2 b2 c2 d2 5
Q3. Apply the BUC
and show all the cells (with measure values) that belong to the iceberg cube.
A B C D count
a1 b1 c1 d1 1
a1 b2 c1 d1 3
a2 b1 c1 d2 1
a2 b2 c2 d2 5
Q3. Apply the BUC algorithm on the following table for minCount=4. You should describe the process
and show all the cells (with measure values) that belong to the iceberg cube.
A B C D count
a1 b1 c1 d1 1
a1 b2 c1 d1 3
a2 b1 c1 d2 1
a2 b2 c2 d2 5
Answer
Bottom-Up Computation Algorithm
BottomUpCube (BUC), a new technique presented by Kevin Beyer and Raghu Ramakrishnan, computes sparse and Iceberg cubes (Beyer and Ramakrishnan 1999). The algorithm is based on those provided in (Ross) Srivastava et al., 1997), which combines partitioning for greater efficiency, prune. Analysis of the BUC's performance. It was shown to be significantly faster than its nearest competitors. In addition, BUC, which has been limited to simple metrics, has been expanded Count and Sum, for example, were expanded in (Han et al. 2001). Iceberg cubes have complex measurements, such as average.
The BUC processing tree in three dimensions is shown in Figure 1. In contrast to previous cube algorithms, BUC starts the cube computation from the most aggregated group-bys and works its way down to the least aggregated.
It's a recursive algorithm that uses minimal support pruning to avoid recursion to lower levels of aggregation (i.e. higher levels in the processing tree) if the mins up conditions aren't met at the present level.
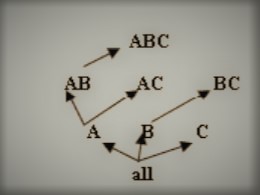
Figure 1.1 Tree of BUC Processing
BUC takes the full input and aggregates it in order to evaluate the supplied measure, such as Count. BUC examines the first attribute dimension A if the value matches the threshold criterion. After that, the input is ordered by A and partitioned to get the count of each distinct value of A. When the count of a given attribute value x exceeds minsup, the value is considered frequent and is output to the results. As a result, BUC investigates the tuples containing x in the first attribute of the input relation. The new input to BUC's recursive call is made up of those tuples.
The following dimension, B, is then ordered and partitioned. In a new recursive call on dimension C, only the tuples with frequent attribute values of B in the current input are examined. The frequent combinations discovered throughout the recursive process are forwarded to output. The method recurses back to the previous level and evaluates the next attribute value of B after all attribute values in the last dimension have been reviewed. BUC also recurses back to dimension A to evaluate the next attribute value of A after considering all of B's attribute values. Finally, the method returns when no more frequent counts can be detected and the output relation contains all common combinations.
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 10 images









