Another instance when people are likely not to spend a dime (or a minute) on an item is when they have a dislike for mixing the item with other items available. In this case, we say the consumer has ‘non-convex preferences’ and indifference curves are bowed out from the origin. In plain language, the consumer has a preference for binging. We often feel this way towards our favorite social media app. Consider a kid who has four hours a day to spend on social media. They enjoy spending time on Snapchat (x) or spending time on Twitter (y). a) Write the kid’s time constraint and illustrate it in a graph where you measure time spent on Snapchat along the horizontal axis and time spent on Twitter along the vertical axis. This kid’s utility from time spent on Snapchat and time spent on Twitter is U(x,y) = 4x2+ y2. b) In your graph, draw a couple of the kid’s indifference curves. Notice how the kid’s |MRSY,X| increases along each curve as he spends more time on Snapchat and less time on Twitter. c) Geometrically, find the kid’s optimal time-allocation, that is the point on the kid’s time constraint that lies on the highest possible indifference curve. Does the kid spend any time on Twitter?
Another instance when people are likely not to spend a dime (or a minute) on an item is when they have a dislike for mixing the item with other items available. In this case, we say the consumer has ‘non-convex preferences’ and indifference curves are bowed out from the origin. In plain language, the consumer has a preference for binging. We often feel this way towards our favorite social media app.
Consider a kid who has four hours a day to spend on social media. They enjoy spending time on Snapchat (x) or spending time on Twitter (y).
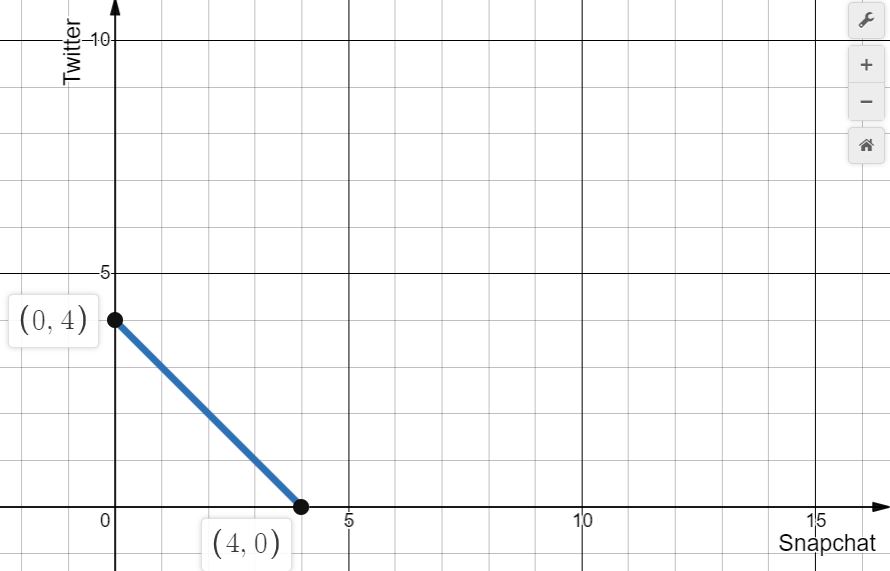
a) Write the kid’s time constraint and illustrate it in a graph where you measure time spent on Snapchat along the horizontal axis and time spent on Twitter along the vertical axis. This kid’s utility from time spent on Snapchat and time spent on Twitter is U(x,y) = 4x2+ y2.
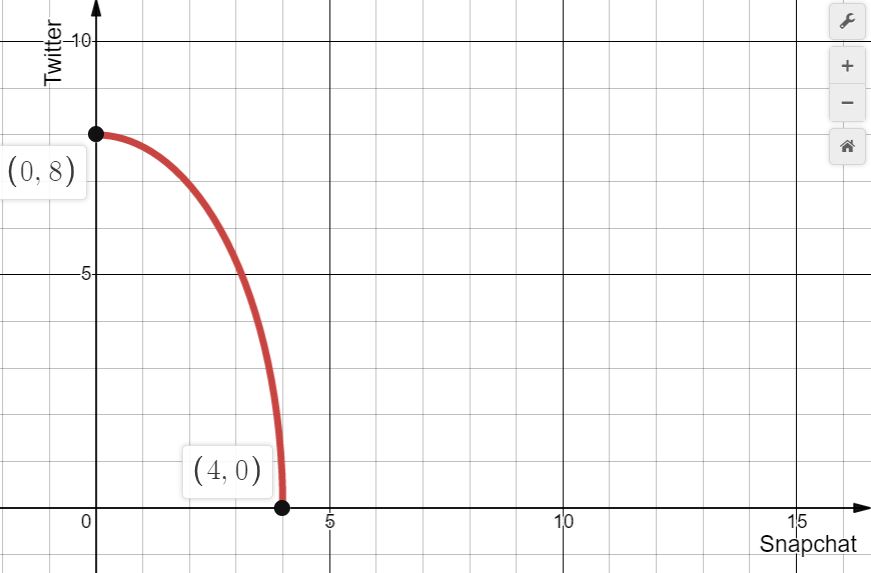
b) In your graph, draw a couple of the kid’s indifference curves. Notice how the kid’s |MRSY,X| increases along each curve as he spends more time on Snapchat and less time on Twitter.
c) Geometrically, find the kid’s optimal time-allocation, that is the point on the kid’s time constraint that lies on the highest possible indifference curve. Does the kid spend any time on Twitter?
d) Last, check that the Lagrangian method would fail to find the correct optimal time allocation.
a. Write the Lagrangian function. Goal function first followed by the time constraint pre-multiplied by negative lamda.
b. Write the first order conditions for the Lagrangian (derivatives respect to x, to y, and to l equated to zero) and solve. Do you find acceptable values for x, y and l? Why do you think they are the wrong ones?
“Since you have posted a question with multiple sub-parts, we will solve the first three subparts for you. To get the remaining sub-parts solved, please repost the complete question and mention the sub-parts to be solved.”.
Part A) This kid has non-convex preferences as given in the question. Let
x: time spent on Snapchat
y: time spent on twitter
Total number of hours available to be spent on social media platforms = 4 hours
Hence, the time constraint for this kid is mathematically represented below:
Since the preferences are non-convex this will always yield corner solution as optimal preferences – implies kid always wants to spend time either on Snapchat or on twitter.
Trending now
This is a popular solution!
Step by step
Solved in 3 steps with 6 images









