An object is placed (3.80x10^1) cm in front of a spherical mirror.-- An "upright" image is formed that is twice as tall as the object. You must do BOTH of the following. FIRST determine the radius of curvature of the mirror in cm to 3 significant digits Be certain to include the appropriate "sign" for the focal length.
An object is placed (3.80x10^1) cm in front of a spherical mirror.-- An "upright" image is formed that is twice as tall as the object. You must do BOTH of the following. FIRST determine the radius of curvature of the mirror in cm to 3 significant digits Be certain to include the appropriate "sign" for the focal length.
Given object is put in front of a spherical mirror at distance 3.80x101cm
The image is upright two times to the object.
Since the image is larger than the size of the object and it's upright therefore the spherical mirror must be a concave mirror.
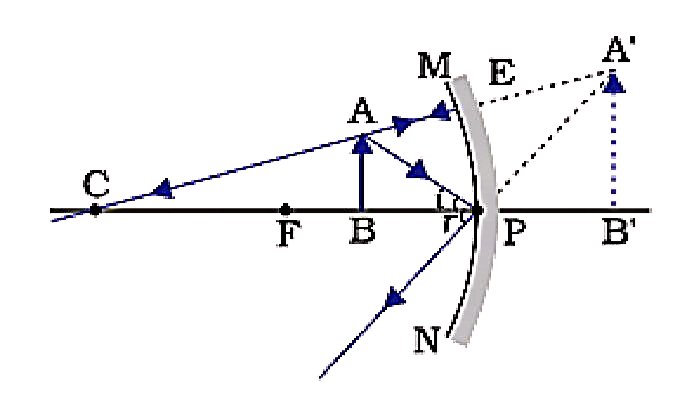
Here AB=object, A'B'= image
Let's assume height of image is h and height of object is h' then as per question
.gif)
But we know from spherical mirror relation
.gif)
With v=distance of image, and u=distance of the object.
And u=-3.80x101cm
Therefore
.gif)
Step by step
Solved in 4 steps with 5 images
