An important concern in the study of heat transfer is to determine the steady-state temperature distribution of a thin plate when the temperature around the boundary is known. Assume the plate shown in the figure represents a cross section of a metal beam, with negligible heat flow in the direction perpendicular to the plate. Let T₁,..., T4 denote the temperatures at the four interior nodes of the mesh in the figure. The temperature at a node is approximately equal to the average of the four nearest nodes- to the left, above, to the right, and below.? For instance, T₁ = (10+20+ T₂+ T4)/4, or 4T₁ T₂-T4 = 30 20° 20° 10° 10° 2 4 3 30° 30° - 40° 40° 33. Write a system of four equations whose solution gives esti- mates for the temperatures T₁,..., T4. 301
An important concern in the study of heat transfer is to determine the steady-state temperature distribution of a thin plate when the temperature around the boundary is known. Assume the plate shown in the figure represents a cross section of a metal beam, with negligible heat flow in the direction perpendicular to the plate. Let T₁,..., T4 denote the temperatures at the four interior nodes of the mesh in the figure. The temperature at a node is approximately equal to the average of the four nearest nodes- to the left, above, to the right, and below.? For instance, T₁ = (10+20+ T₂+ T4)/4, or 4T₁ T₂-T4 = 30 20° 20° 10° 10° 2 4 3 30° 30° - 40° 40° 33. Write a system of four equations whose solution gives esti- mates for the temperatures T₁,..., T4. 301
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
33 please
![23. a. Every elementary row operation is reversible.
b. A 5 x 6 matrix has six rows.
c. The solution set of a linear system involving variables
X₁,..., X, is a list of numbers (s₁,..., Sn) that makes each
equation in the system a true statement when the values
S₁,..., S, are substituted for x₁,..., Xn, respectively.
d. Two fundamental questions about a linear system involve
existence and uniqueness.
24. a. Elementary row operations on an augmented matrix never
change the solution set of the associated linear system.
b. Two matrices are row equivalent if they have the same
number of rows.
c. An inconsistent system has more than one solution.
d. Two linear systems are equivalent if they have the same
solution set.
25. Find an equation involving g, h, and k that makes this
augmented matrix correspond to a consistent system:
1
0
-2
−4
3
5
7
-5
-9
26. Construct three different augmented matrices for linear sys-
tems whose solution set is x₁ = -2, x₂ = 1, X3 = 0.
g
h
k
27. Suppose the system below is consistent for all possible values
of f and g. What can you say about the coefficients c and d?
Justify your answer.
x₁ + 3x₂ = f
cx₁ + dx₂ = g
28. Suppose a, b, c, and d are constants such that a is not zero
and the system below is consistent for all possible values of
f and g. What can you say about the numbers a, b, c, and d?
Justify your answer.
ax₁ + bx₂ = f
cx₁ + dx₂ = g
In Exercises 29-32, find the elementary row operation that trans-
forms the first matrix into the second, and then find the reverse
row operation that transforms the second matrix into the first.
29.
30.
31.
32.
0-2
-00 0
1
3 -1
5
4 -7
6
101
* * * * * * * * *
0 -5
12
3-4
-2
1 -2
0
0
4 - 1
6
9
5 -2
مناسب
-3
3
1 2 -5
1.1 Systems of Linear Equations 11
0
1 -3 -2
9 5
0
8
-6
10°
4 -7
5
6
100
10°
-2
0
3 -1
*~-~-4
3
-5
1 -2 1
0 5 -2
0
1
0
0
-4
-3
9
1
* * * -
4
7 -1
An important concern in the study of heat transfer is to determine
the steady-state temperature distribution of a thin plate when the
temperature around the boundary is known. Assume the plate
shown in the figure represents a cross section of a metal beam,
with negligible heat flow in the direction perpendicular to the
plate. Let T₁,..., T4 denote the temperatures at the four interior
nodes of the mesh in the figure. The temperature at a node is
approximately equal to the average of the four nearest nodes-
to the left, above, to the right, and below. For instance,
2
-5
1-3-2
0 -1
T₁ = (10 + 20+ T₂+ T4)/4, or 4T₁-T₂-T4 = 30
20° 20°
0 0
0
8
-6
0
2
3
30° 30°
40°
40°
33. Write a system of four equations whose solution gives esti-
mates for the temperatures T₁,..., T4.
34. Solve the system of equations from Exercise 33. [Hint: To
speed up the calculations, interchange rows 1 and 4 before
starting "replace" operations.]
See Frank M. White, Heat and Mass Transfer (Reading, MA:
Addison-Wesley Publishing, 1991), pp. 145-149.
SOLUTIONS TO PRACTICE PROBLEMS
1. a. For "hand computation," the best choice is to interchange equations 3 and 4.
Another possibility is to multiply equation 3 by 1/5. Or, replace equation 4 by
its sum with -1/5 times row 3. (In any case, do not use the x₂ in equation 2 to
eliminate the 4x2 in equation 1. Wait until a triangular form has been reached and
the x3 terms and x4 terms have been eliminated from the first two equations.)
b. The system is in triangular form. Further simplification begins with the x4 in the
fourth equation. Use the x4 to eliminate all x4 terms above it. The appropriate](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F1bfb7105-3383-49f1-9e7c-a22283ce619a%2Fe3e8bab4-9de8-4bfa-a4cf-92bda984d5ed%2Fbc58x2b_processed.jpeg&w=3840&q=75)
Transcribed Image Text:23. a. Every elementary row operation is reversible.
b. A 5 x 6 matrix has six rows.
c. The solution set of a linear system involving variables
X₁,..., X, is a list of numbers (s₁,..., Sn) that makes each
equation in the system a true statement when the values
S₁,..., S, are substituted for x₁,..., Xn, respectively.
d. Two fundamental questions about a linear system involve
existence and uniqueness.
24. a. Elementary row operations on an augmented matrix never
change the solution set of the associated linear system.
b. Two matrices are row equivalent if they have the same
number of rows.
c. An inconsistent system has more than one solution.
d. Two linear systems are equivalent if they have the same
solution set.
25. Find an equation involving g, h, and k that makes this
augmented matrix correspond to a consistent system:
1
0
-2
−4
3
5
7
-5
-9
26. Construct three different augmented matrices for linear sys-
tems whose solution set is x₁ = -2, x₂ = 1, X3 = 0.
g
h
k
27. Suppose the system below is consistent for all possible values
of f and g. What can you say about the coefficients c and d?
Justify your answer.
x₁ + 3x₂ = f
cx₁ + dx₂ = g
28. Suppose a, b, c, and d are constants such that a is not zero
and the system below is consistent for all possible values of
f and g. What can you say about the numbers a, b, c, and d?
Justify your answer.
ax₁ + bx₂ = f
cx₁ + dx₂ = g
In Exercises 29-32, find the elementary row operation that trans-
forms the first matrix into the second, and then find the reverse
row operation that transforms the second matrix into the first.
29.
30.
31.
32.
0-2
-00 0
1
3 -1
5
4 -7
6
101
* * * * * * * * *
0 -5
12
3-4
-2
1 -2
0
0
4 - 1
6
9
5 -2
مناسب
-3
3
1 2 -5
1.1 Systems of Linear Equations 11
0
1 -3 -2
9 5
0
8
-6
10°
4 -7
5
6
100
10°
-2
0
3 -1
*~-~-4
3
-5
1 -2 1
0 5 -2
0
1
0
0
-4
-3
9
1
* * * -
4
7 -1
An important concern in the study of heat transfer is to determine
the steady-state temperature distribution of a thin plate when the
temperature around the boundary is known. Assume the plate
shown in the figure represents a cross section of a metal beam,
with negligible heat flow in the direction perpendicular to the
plate. Let T₁,..., T4 denote the temperatures at the four interior
nodes of the mesh in the figure. The temperature at a node is
approximately equal to the average of the four nearest nodes-
to the left, above, to the right, and below. For instance,
2
-5
1-3-2
0 -1
T₁ = (10 + 20+ T₂+ T4)/4, or 4T₁-T₂-T4 = 30
20° 20°
0 0
0
8
-6
0
2
3
30° 30°
40°
40°
33. Write a system of four equations whose solution gives esti-
mates for the temperatures T₁,..., T4.
34. Solve the system of equations from Exercise 33. [Hint: To
speed up the calculations, interchange rows 1 and 4 before
starting "replace" operations.]
See Frank M. White, Heat and Mass Transfer (Reading, MA:
Addison-Wesley Publishing, 1991), pp. 145-149.
SOLUTIONS TO PRACTICE PROBLEMS
1. a. For "hand computation," the best choice is to interchange equations 3 and 4.
Another possibility is to multiply equation 3 by 1/5. Or, replace equation 4 by
its sum with -1/5 times row 3. (In any case, do not use the x₂ in equation 2 to
eliminate the 4x2 in equation 1. Wait until a triangular form has been reached and
the x3 terms and x4 terms have been eliminated from the first two equations.)
b. The system is in triangular form. Further simplification begins with the x4 in the
fourth equation. Use the x4 to eliminate all x4 terms above it. The appropriate
Expert Solution
Step 1
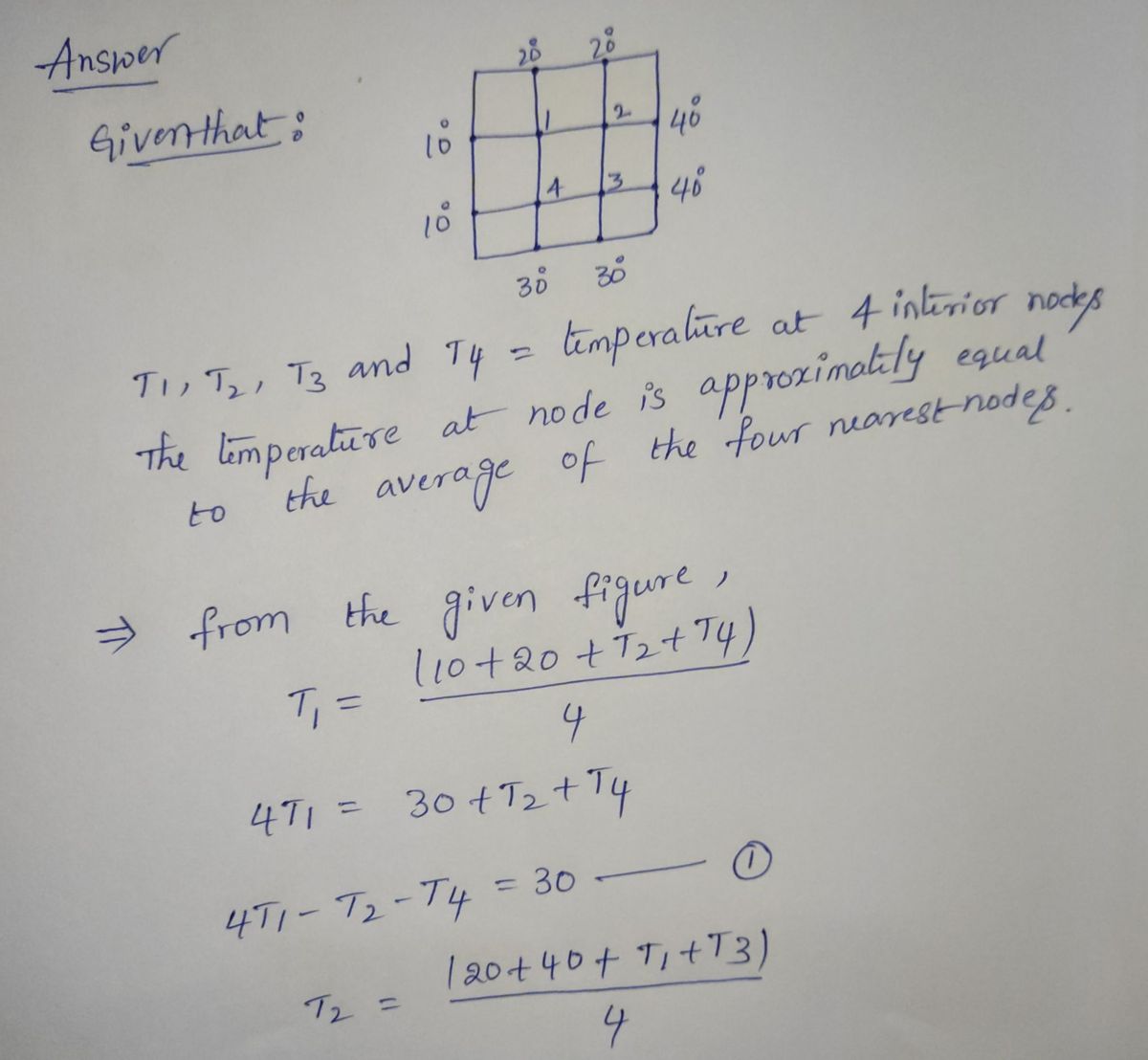
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

