The image presents a graph of a trigonometric function plotted on a Cartesian coordinate system, with the x-axis and y-axis labeled. The function appears to be a sine or cosine wave, given its periodic nature and symmetry. **Key Details:** 1. **Axes:** - The horizontal axis is the x-axis. - The vertical axis is the y-axis. 2. **Points:** - The graph passes through several notable points, including: - \((-π, 0)\) - \((-π/2, -1)\) - \((0, 0)\) - \((π/2, 1)\) - \((π, 0)\) 3. **Shape:** - The waveform shows typical characteristics of a sine or cosine function, oscillating between 1 and -1. - It crosses the x-axis at \(-π\), \(0\), and \(π\). - The function reaches a minimum of -1 at \((-π/2, -1)\) and a maximum of 1 at \((π/2, 1)\). **Text Overlay:** Below the graph, the text indicates a question: "Select the correct choice below and fill in any answer boxes within your choice. Use a comma to separate answers as needed." This suggests an interactive component or question related to identifying critical points or analyzing the graph further. ### Using the Given Graph of the Function \( f \), Find the Following: #### (a) Local Maxima - **Problem:** Identify the numbers, if any, at which the function \( f \) has a local maximum. Determine what these local maxima are. #### (b) Local Minima - **Problem:** Identify the numbers, if any, at which the function \( f \) has a local minimum. Determine what these local minima are. --- ### To Solve: #### (a) Finding Local Maxima - **Instructions:** Find the value(s) of \( x \) at which \( f \) has a local maximum. - **Options:** - **A.** \( x = \) (Provide an exact answer, using \(\pi\) as needed.) - **B.** There is no solution. - **Selection:** Choose the correct option for the local maximum from the choices provided. ### Visual Explanation: - There is an implicit reference to a graph of function \( f \) not visible here. To find local maxima or minima, identify points where the function changes direction from increasing to decreasing or vice versa, respectively.
The image presents a graph of a trigonometric function plotted on a Cartesian coordinate system, with the x-axis and y-axis labeled. The function appears to be a sine or cosine wave, given its periodic nature and symmetry. **Key Details:** 1. **Axes:** - The horizontal axis is the x-axis. - The vertical axis is the y-axis. 2. **Points:** - The graph passes through several notable points, including: - \((-π, 0)\) - \((-π/2, -1)\) - \((0, 0)\) - \((π/2, 1)\) - \((π, 0)\) 3. **Shape:** - The waveform shows typical characteristics of a sine or cosine function, oscillating between 1 and -1. - It crosses the x-axis at \(-π\), \(0\), and \(π\). - The function reaches a minimum of -1 at \((-π/2, -1)\) and a maximum of 1 at \((π/2, 1)\). **Text Overlay:** Below the graph, the text indicates a question: "Select the correct choice below and fill in any answer boxes within your choice. Use a comma to separate answers as needed." This suggests an interactive component or question related to identifying critical points or analyzing the graph further. ### Using the Given Graph of the Function \( f \), Find the Following: #### (a) Local Maxima - **Problem:** Identify the numbers, if any, at which the function \( f \) has a local maximum. Determine what these local maxima are. #### (b) Local Minima - **Problem:** Identify the numbers, if any, at which the function \( f \) has a local minimum. Determine what these local minima are. --- ### To Solve: #### (a) Finding Local Maxima - **Instructions:** Find the value(s) of \( x \) at which \( f \) has a local maximum. - **Options:** - **A.** \( x = \) (Provide an exact answer, using \(\pi\) as needed.) - **B.** There is no solution. - **Selection:** Choose the correct option for the local maximum from the choices provided. ### Visual Explanation: - There is an implicit reference to a graph of function \( f \) not visible here. To find local maxima or minima, identify points where the function changes direction from increasing to decreasing or vice versa, respectively.
Algebra and Trigonometry (6th Edition)
6th Edition
ISBN:9780134463216
Author:Robert F. Blitzer
Publisher:Robert F. Blitzer
ChapterP: Prerequisites: Fundamental Concepts Of Algebra
Section: Chapter Questions
Problem 1MCCP: In Exercises 1-25, simplify the given expression or perform the indicated operation (and simplify,...
Related questions
Topic Video
Question
100%
Im really confused and don't know how to do this.

Transcribed Image Text:The image presents a graph of a trigonometric function plotted on a Cartesian coordinate system, with the x-axis and y-axis labeled. The function appears to be a sine or cosine wave, given its periodic nature and symmetry.
**Key Details:**
1. **Axes:**
- The horizontal axis is the x-axis.
- The vertical axis is the y-axis.
2. **Points:**
- The graph passes through several notable points, including:
- \((-π, 0)\)
- \((-π/2, -1)\)
- \((0, 0)\)
- \((π/2, 1)\)
- \((π, 0)\)
3. **Shape:**
- The waveform shows typical characteristics of a sine or cosine function, oscillating between 1 and -1.
- It crosses the x-axis at \(-π\), \(0\), and \(π\).
- The function reaches a minimum of -1 at \((-π/2, -1)\) and a maximum of 1 at \((π/2, 1)\).
**Text Overlay:**
Below the graph, the text indicates a question:
"Select the correct choice below and fill in any answer boxes within your choice. Use a comma to separate answers as needed."
This suggests an interactive component or question related to identifying critical points or analyzing the graph further.

Transcribed Image Text:### Using the Given Graph of the Function \( f \), Find the Following:
#### (a) Local Maxima
- **Problem:** Identify the numbers, if any, at which the function \( f \) has a local maximum. Determine what these local maxima are.
#### (b) Local Minima
- **Problem:** Identify the numbers, if any, at which the function \( f \) has a local minimum. Determine what these local minima are.
---
### To Solve:
#### (a) Finding Local Maxima
- **Instructions:** Find the value(s) of \( x \) at which \( f \) has a local maximum.
- **Options:**
- **A.** \( x = \) (Provide an exact answer, using \(\pi\) as needed.)
- **B.** There is no solution.
- **Selection:** Choose the correct option for the local maximum from the choices provided.
### Visual Explanation:
- There is an implicit reference to a graph of function \( f \) not visible here. To find local maxima or minima, identify points where the function changes direction from increasing to decreasing or vice versa, respectively.
Expert Solution
Concept used
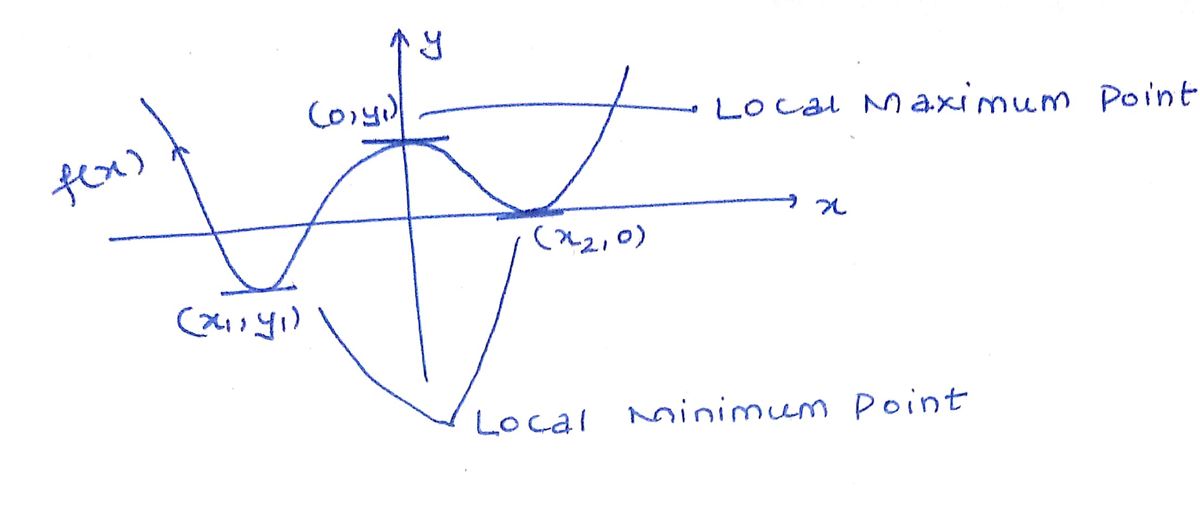
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 2 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, algebra and related others by exploring similar questions and additional content below.Recommended textbooks for you

Algebra and Trigonometry (6th Edition)
Algebra
ISBN:
9780134463216
Author:
Robert F. Blitzer
Publisher:
PEARSON

Contemporary Abstract Algebra
Algebra
ISBN:
9781305657960
Author:
Joseph Gallian
Publisher:
Cengage Learning

Linear Algebra: A Modern Introduction
Algebra
ISBN:
9781285463247
Author:
David Poole
Publisher:
Cengage Learning

Algebra and Trigonometry (6th Edition)
Algebra
ISBN:
9780134463216
Author:
Robert F. Blitzer
Publisher:
PEARSON

Contemporary Abstract Algebra
Algebra
ISBN:
9781305657960
Author:
Joseph Gallian
Publisher:
Cengage Learning

Linear Algebra: A Modern Introduction
Algebra
ISBN:
9781285463247
Author:
David Poole
Publisher:
Cengage Learning

Algebra And Trigonometry (11th Edition)
Algebra
ISBN:
9780135163078
Author:
Michael Sullivan
Publisher:
PEARSON

Introduction to Linear Algebra, Fifth Edition
Algebra
ISBN:
9780980232776
Author:
Gilbert Strang
Publisher:
Wellesley-Cambridge Press

College Algebra (Collegiate Math)
Algebra
ISBN:
9780077836344
Author:
Julie Miller, Donna Gerken
Publisher:
McGraw-Hill Education