The image contains a coordinate plane graph along with a system of linear inequalities. ### System of Inequalities: 1. \(-x - 2y \leq 6\) 2. \(-2x - 6y \geq 12\) ### Description of the Graph: The graph is a coordinate plane where both the x-axis and y-axis range from -7 to 7. The units on both axes increase by 1. - **First Inequality (\(-x - 2y \leq 6\)):** - This inequality represents a line and a half-plane. The line itself is not plotted, but its boundary would be expressed as \(x + 2y = -6\). The area of interest would be below this line, given the direction of the inequality. - **Second Inequality (\(-2x - 6y \geq 12\)):** - This inequality represents another line and its accompanying half-plane. The boundary line could be expressed as \(2x + 6y = -12\). The area of interest would be above this line, as indicated by the inequality. ### Explanation for Educational Context: To solve this system graphically, students would draw the lines represented by the equalities \(x + 2y = -6\) and \(2x + 6y = -12\) on the graph. They would then identify the solution region that satisfies both inequalities simultaneously, often a common overlapping area that meets the criteria of being below the first line and above the second. This exercise helps with understanding graphical solutions to systems of inequalities and visualizing feasible regions.
The image contains a coordinate plane graph along with a system of linear inequalities. ### System of Inequalities: 1. \(-x - 2y \leq 6\) 2. \(-2x - 6y \geq 12\) ### Description of the Graph: The graph is a coordinate plane where both the x-axis and y-axis range from -7 to 7. The units on both axes increase by 1. - **First Inequality (\(-x - 2y \leq 6\)):** - This inequality represents a line and a half-plane. The line itself is not plotted, but its boundary would be expressed as \(x + 2y = -6\). The area of interest would be below this line, given the direction of the inequality. - **Second Inequality (\(-2x - 6y \geq 12\)):** - This inequality represents another line and its accompanying half-plane. The boundary line could be expressed as \(2x + 6y = -12\). The area of interest would be above this line, as indicated by the inequality. ### Explanation for Educational Context: To solve this system graphically, students would draw the lines represented by the equalities \(x + 2y = -6\) and \(2x + 6y = -12\) on the graph. They would then identify the solution region that satisfies both inequalities simultaneously, often a common overlapping area that meets the criteria of being below the first line and above the second. This exercise helps with understanding graphical solutions to systems of inequalities and visualizing feasible regions.
Algebra and Trigonometry (6th Edition)
6th Edition
ISBN:9780134463216
Author:Robert F. Blitzer
Publisher:Robert F. Blitzer
ChapterP: Prerequisites: Fundamental Concepts Of Algebra
Section: Chapter Questions
Problem 1MCCP: In Exercises 1-25, simplify the given expression or perform the indicated operation (and simplify,...
Related questions
Question

Transcribed Image Text:The image contains a coordinate plane graph along with a system of linear inequalities.
### System of Inequalities:
1. \(-x - 2y \leq 6\)
2. \(-2x - 6y \geq 12\)
### Description of the Graph:
The graph is a coordinate plane where both the x-axis and y-axis range from -7 to 7. The units on both axes increase by 1.
- **First Inequality (\(-x - 2y \leq 6\)):**
- This inequality represents a line and a half-plane. The line itself is not plotted, but its boundary would be expressed as \(x + 2y = -6\). The area of interest would be below this line, given the direction of the inequality.
- **Second Inequality (\(-2x - 6y \geq 12\)):**
- This inequality represents another line and its accompanying half-plane. The boundary line could be expressed as \(2x + 6y = -12\). The area of interest would be above this line, as indicated by the inequality.
### Explanation for Educational Context:
To solve this system graphically, students would draw the lines represented by the equalities \(x + 2y = -6\) and \(2x + 6y = -12\) on the graph. They would then identify the solution region that satisfies both inequalities simultaneously, often a common overlapping area that meets the criteria of being below the first line and above the second. This exercise helps with understanding graphical solutions to systems of inequalities and visualizing feasible regions.
Expert Solution
Basic
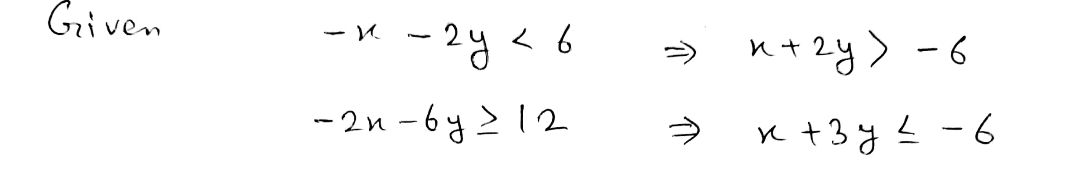
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Algebra and Trigonometry (6th Edition)
Algebra
ISBN:
9780134463216
Author:
Robert F. Blitzer
Publisher:
PEARSON

Contemporary Abstract Algebra
Algebra
ISBN:
9781305657960
Author:
Joseph Gallian
Publisher:
Cengage Learning

Linear Algebra: A Modern Introduction
Algebra
ISBN:
9781285463247
Author:
David Poole
Publisher:
Cengage Learning

Algebra and Trigonometry (6th Edition)
Algebra
ISBN:
9780134463216
Author:
Robert F. Blitzer
Publisher:
PEARSON

Contemporary Abstract Algebra
Algebra
ISBN:
9781305657960
Author:
Joseph Gallian
Publisher:
Cengage Learning

Linear Algebra: A Modern Introduction
Algebra
ISBN:
9781285463247
Author:
David Poole
Publisher:
Cengage Learning

Algebra And Trigonometry (11th Edition)
Algebra
ISBN:
9780135163078
Author:
Michael Sullivan
Publisher:
PEARSON

Introduction to Linear Algebra, Fifth Edition
Algebra
ISBN:
9780980232776
Author:
Gilbert Strang
Publisher:
Wellesley-Cambridge Press

College Algebra (Collegiate Math)
Algebra
ISBN:
9780077836344
Author:
Julie Miller, Donna Gerken
Publisher:
McGraw-Hill Education