3)Find the first partial derivatives of the functionf(x, y)sin (et) dt=2X

Answered: Image /qna-images/answer/bb5e73c4-54fe-46b0-8684-d53d2e8dbe15.jpg

Answered: 3) Find the first partial derivatives…

Advanced Engineering Mathematics

10th Edition

ISBN:9780470458365

Author:Erwin Kreyszig

Publisher:Erwin Kreyszig

Chapter2: Second-order Linear Odes

Section: Chapter Questions

Problem 1RQ

See similar textbooks

Related questions

Question

3)
Find the first partial derivatives of the function
f(x, y)
sin (et) dt
=
2X

Expert Solution

Step 1

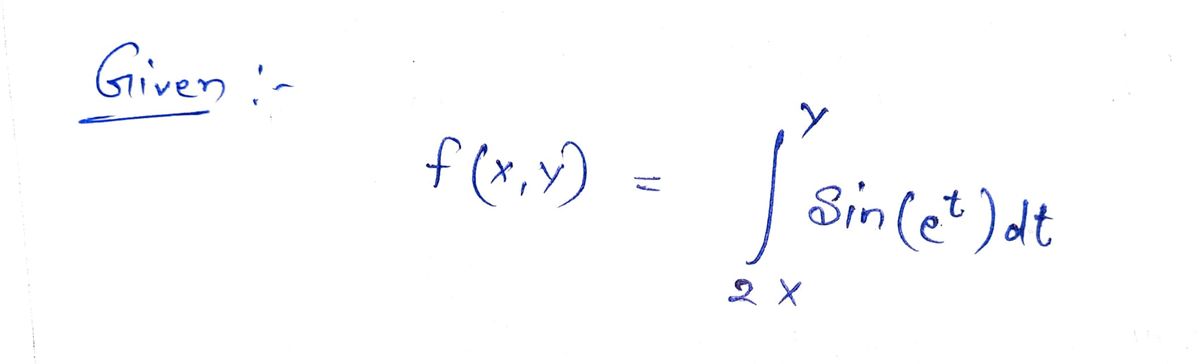
Trending now

This is a popular solution!

Step by step

Solved in 2 steps with 2 images

SEE SOLUTION Check out a sample Q&A here

Follow-up Questions

Read through expert solutions to related follow-up questions below.

Follow-up Question

I thought the derivative of sin(e^2x) was 2e^2xcos(e^2x) but in the answer we just have sin(e^2x)(2x)d/dx. Is that correct?

Solution

by Bartleby Expert

SEE SOLUTION

Follow-up Question

After seeing the additional solution for Fx(x,y), shouldn't it be -2sin(e^2x) instead of positive 2sin(e^2x) since it is Fx = 0 - sin(e^2x)(2)

Solution

by Bartleby Expert

SEE SOLUTION

Follow-up Question

Do I not have to do anything to find the other partial derivative Fx? Or is that just 0? Also does that second part become 0 becuase the d/dy means we take the derivative in respect to y and there are none (only sin(e^2x) and 2x) so it is 0? Sorry for the questions it has been a very long time since I've done any math so I'm struggling a bit to grasp the concepts on this problem. Thanks!

Solution

by Bartleby Expert

SEE SOLUTION

Similar questions