Please draw the diagram for this problem to explain the answer clearly. Please give a detailed explanation of each of the steps in the answer. c) Find the magnetic field in the center of an n-sided polygon loop. (Draw and label your own diagram to help set up theproblem.) bonus 2) Consider pieces of wire, each of length L, that are bent into closed loops in the shapes of regular polygons. Each loopcarries a current I.a) Find the magnetic field in the center of the triangular loop. (Be sure to label the diagram to help set up the problem.)B3b) Find the magnetic field in the center of the square loop. (Draw and label your own diagram to help set up the problem.)

Answered: c) Find the magnetic field in the…

Related questions

Question

Please draw the diagram for this problem to explain the answer clearly. Please give a detailed explanation of each of the steps in the answer.

c) Find the magnetic field in the center of an n-sided polygon loop. (Draw and label your own diagram to help set up the
problem.)

bonus 2) Consider pieces of wire, each of length L, that are bent into closed loops in the shapes of regular polygons. Each loop
carries a current I.
a) Find the magnetic field in the center of the triangular loop. (Be sure to label the diagram to help set up the problem.)
B3
b) Find the magnetic field in the center of the square loop. (Draw and label your own diagram to help set up the problem.)

Expert Solution

Step 1

The magnetic field due to a wire of finite length at a distance $r$ from a wire

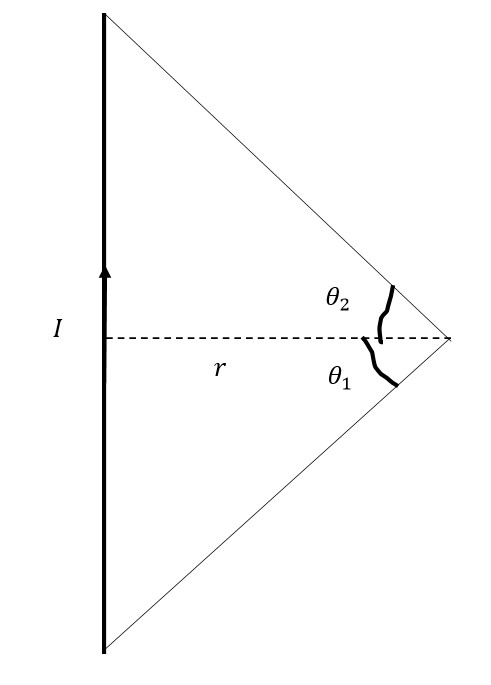
The magnetic field at a distance $r$ from the wire is

$B = \frac{μ_{0} I}{4 π r} (\sin θ_{2} + \sin θ_{1})$

Step 2

a) Let us consider an equilateral triangle of each side $\frac{L}{3}$ as one loop is bent into a shape of a traingle.

$I$ is the current flowing through the wire.

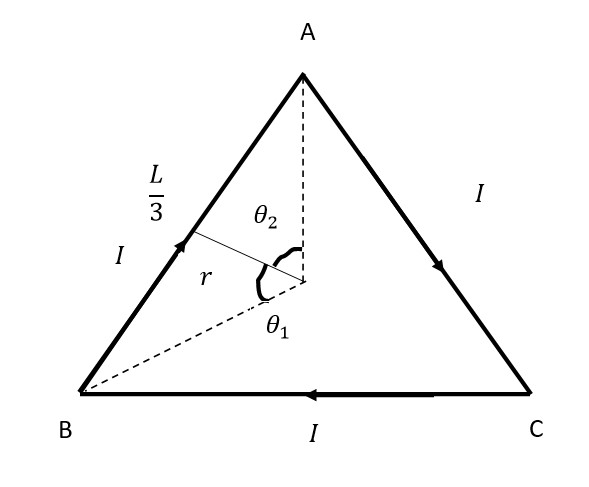
Let us find the magnetic field at the center due to the line segment AB.

The distance of the center of the triangle from the midpoint of side AB is $r = \frac{L}{6 \sqrt{3}}$

Here $θ_{1} = θ_{2} = 60 °$

Thus the magnetic field due to the line AB is

$B_{0} = \frac{μ_{0} I}{4 π r} (\sin θ_{2} + \sin θ_{1}) = \frac{μ_{0} I}{4 π \frac{L}{6 \sqrt{3}}} (\sin 60 ° + \sin 60 °) = \frac{3 \sqrt{3} μ_{0} I}{2 π L} (\frac{\sqrt{3}}{2} + \frac{\sqrt{3}}{2}) = \frac{9 μ_{0} I}{2 π L}$

The field due to the loop is equal to three times the field due to one wire. Thus the magnetic field at the center is

$B = 3 \times B_{0} = 3 \times \frac{9 μ_{0} I}{2 π L} = \frac{27 μ_{0} I}{2 π L}$

b) Each side of the square loop will be of length $\frac{L}{4}$ as the length of the entire wire is of length $L$

$I$ is the current flowing in the square loop

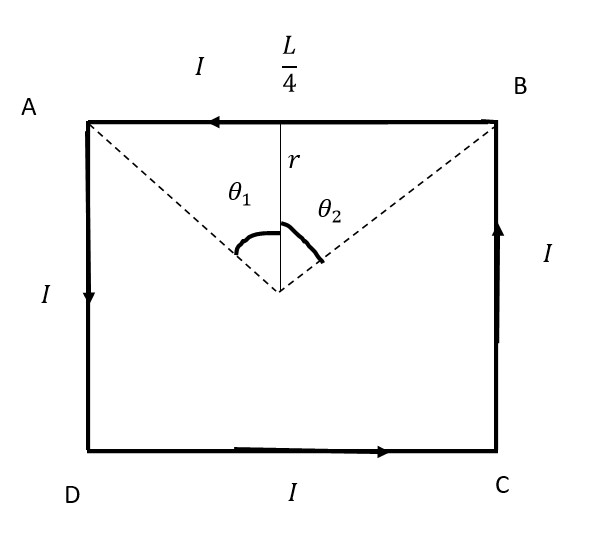
The distance of the wire from the center is $r = \frac{1}{2} (\frac{L}{4}) = \frac{L}{8}$

The measure of the angles $θ_{1} = θ_{2} = 45 °$

The magnetic field due to the line AB on the center of the wire is

$B_{0} = \frac{μ_{0} I}{4 π r} (\sin θ_{2} + \sin θ_{1}) = \frac{μ_{0} I}{4 π \frac{L}{8}} (\sin 45 ° + \sin 45 °) = \frac{2 μ_{0} I}{π L} (\frac{1}{\sqrt{2}} + \frac{1}{\sqrt{2}}) = \frac{2}{\sqrt{2}} \frac{2 μ_{0} I}{π L} = \frac{2 \sqrt{2} μ_{0} I}{π L}$

The magnetic field due to the entire loop is four times due to one loop

$B = 4 \times B_{0} = 4 \times \frac{2 \sqrt{2} μ_{0} I}{π L} = \frac{8 \sqrt{2} μ_{0} I}{π L}$

c) For a n-sided polygon, the length of each side will be $\frac{L}{n}$

$I$ is the current flowing through the polygon.

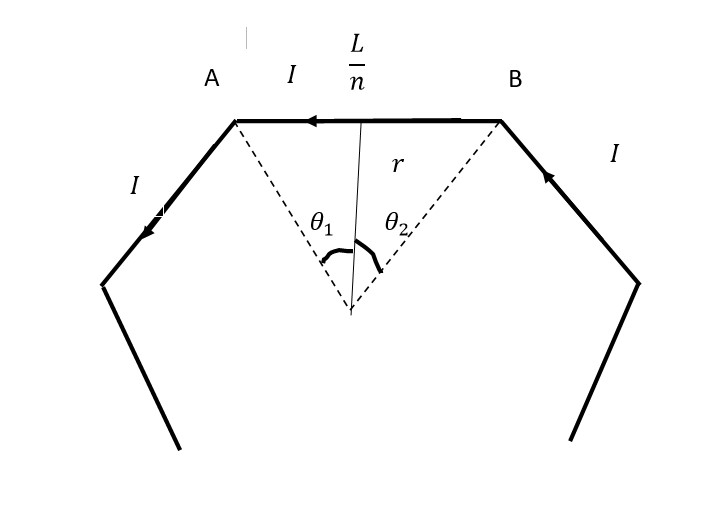
The angles in the diagram $θ_{1} = θ_{2} = \frac{π}{n}$

The measure of the distance of the center from the center of one side $r = \frac{L}{2 n} c o t \frac{π}{n}$

The magnetic field on the center due to the side $A B$ is

$B_{0} = \frac{μ_{0} I}{4 π r} (\sin θ_{2} + \sin θ_{1}) = \frac{μ_{0} I}{4 π \frac{L}{2 n} c o t \frac{π}{n}} (\sin \frac{π}{n} + \sin \frac{π}{n}) = \frac{2 n μ_{0} I}{4 π L \frac{\cos \frac{π}{n}}{\sin \frac{π}{n}}} 2 \sin \frac{π}{n} = \frac{n μ_{0} I}{π L} \frac{\sin^{2} \frac{π}{n}}{\cos \frac{π}{n}}$

Therefore for n sided polygon, the total magnetic field is

$B = n \times B_{0} = \frac{n^{2} μ_{0} I}{π L} \frac{\sin^{2} \frac{π}{n}}{\cos \frac{π}{n}}$

Step by step

Solved in 3 steps with 4 images