according to a recent survey 85% of voters are in favor of moving election day from the tuesday following the first monday in nov to april 16. If a sample of 13 voters is taken what is the probability that 10 would be in favor of moving election day to April 16?
according to a recent survey 85% of voters are in favor of moving election day from the tuesday following the first monday in nov to april 16. If a sample of 13 voters is taken what is the
Binomial distribution:
A random variable is said to follow binomial distribution if it satisfies the criteria given below:
- The number of observations or trails must be fixed.
- Each observation or trail must be independent.
- The probability of success must be same for all the trails.
The pmf for the binomial distribution or the probability of obtaining x successes in n independent trails of a binomial experiment is,
P(x) = nCx * px * (1 – p)n–x. Where x = 0, 1, 2, …, n and 0 < p < 1.
Here, it is given that, 85% of voters are in favour of moving Election Day to April 16.
The probability of success (Voters in favour of moving Election Day to April 16) is p = 85/100 = 0.85.
The probability of failure (Voters not in favour of moving Election Day to April 16) is 1 – p = 0.15.
The sample number of voters selected is n = 13 (Which is large in size).
The variable x is the number of voters in favour of moving Election Day to April 16.
- Here, the number of voters selected is n = 13, which is fixed.
- Each of the selected 13 voters are independent of each other.
The probability of success (Voters in favour of moving Election Day to April 16) is p = 0.85 (Same for all 13 voters).
Find the probability that 10 voters are in favour of moving Election Day to April 16:
Here, the variable number of voters in favour of moving Election Day to April 16 is 10. That is, x = 10.
The probability that 10 voters are in favour of moving Election Day to April 16 is obtained as 0.19 from the calculation given below:
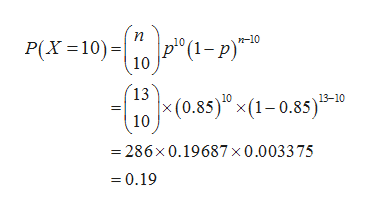
Step by step
Solved in 3 steps with 1 images









