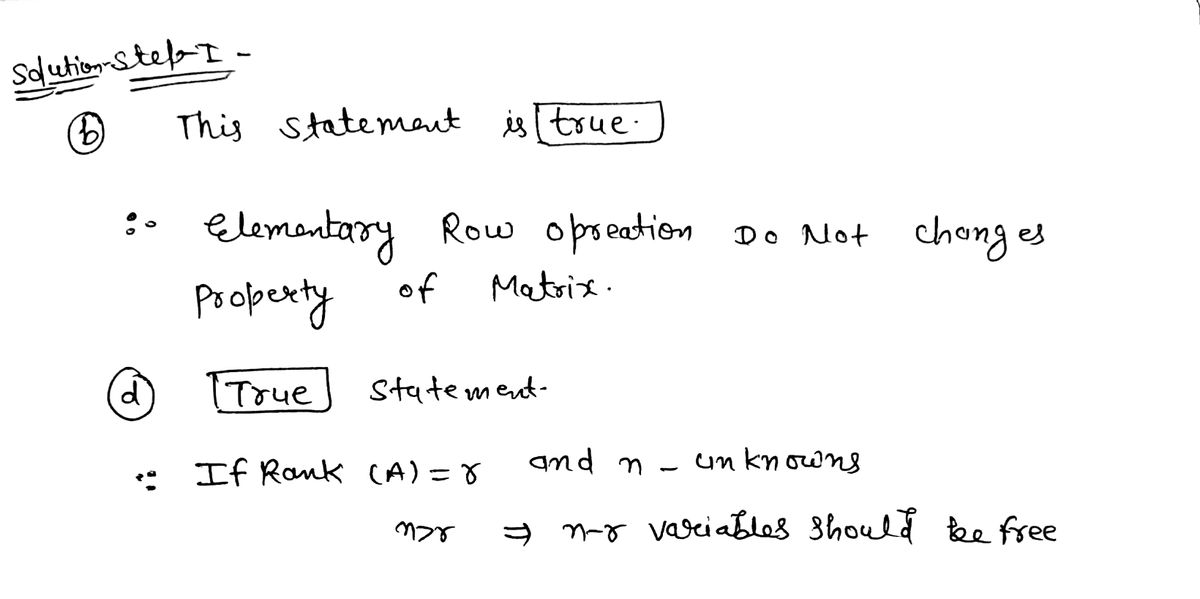
a. If a matrix is in reduced row echelon form, then it is also in row echelon form. b. If an elementary row operation is applied to a matrix that is in row echelon form, the resulting matrix will still be in row echelon form. c. Every matrix has a unique row echelon form. d. A homogeneous linear system in n unknowns whose cor- responding augmented matrix has a reduced row echelon form with r leading 1's has n - r free variables.
a. If a matrix is in reduced row echelon form, then it is also in row echelon form. b. If an elementary row operation is applied to a matrix that is in row echelon form, the resulting matrix will still be in row echelon form. c. Every matrix has a unique row echelon form. d. A homogeneous linear system in n unknowns whose cor- responding augmented matrix has a reduced row echelon form with r leading 1's has n - r free variables.
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
please send handwritten solution
True False b d g i only
handwritten solution please

Transcribed Image Text:True-False Exercises
TF. In parts (a)-(i) determine whether the statement is true or
false, and justify your answer.
a. If a matrix is in reduced row echelon form, then it is also
in row echelon form.
b. If an elementary row operation is applied to a matrix that
is in row echelon form, the resulting matrix will still be in
row echelon form.
c. Every matrix has a unique row echelon form.
d. A homogeneous linear system in n unknowns whose cor-
responding augmented matrix has a reduced row echelon
form with r leading 1's has n - r free variables.
e. All leading 1's in a matrix in row echelon form must occur
in different columns.
f. If every column of a matrix in row echelon form has a
leading 1, then all entries that are not leading 1's are zero.
g. If a homogeneous linear system of n equations in n
unknowns has a corresponding augmented matrix with a
reduced row echelon form containing n leading 1's, then
the linear system has only the trivial solution.
h. If the reduced row echelon form of the augmented matrix
for a linear system has a row of zeros, then the system
must have infinitely many solutions.
i. If a linear system has more unknowns than equations,
then it must have infinitely many solutions.
Expert Solution
Step 1
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

