Homework Help is Here – Start Your Trial Now!
Math
Calculus
a. i=4 2 i=1 b. lim X48 i +1 3 5+2-* c. lim 848 3 5 + 2x drug and

a. i=4 2 i=1 b. lim X48 i +1 3 5+2-* c. lim 848 3 5 + 2x drug and

Calculus: Early Transcendentals
Calculus: Early Transcendentals
8th Edition
ISBN:9781285741550
Author:James Stewart
Publisher:James Stewart
Chapter1: Functions And Models
Section: Chapter Questions
Problem 1RCC: (a) What is a function? What are its domain and range? (b) What is the graph of a function? (c) How...
See similar textbooks
icon
Related questions
Question
Certainly! Here’s a transcription and explanation suitable for an educational website: --- ### Mathematical Expressions **a.** Evaluate the summation: \[ \sum_{i=1}^{4} \frac{2}{i + 1} \] This expression represents the sum of terms where each term is calculated as \(\frac{2}{i + 1}\), with the index \(i\) ranging from 1 to 4. **b.** Calculate the limit: \[ \lim_{x \to \infty} \frac{3}{5 + 2^{-x}} \] Here, the expression asks for the limit of the fraction \(\frac{3}{5 + 2^{-x}}\) as \(x\) approaches infinity. **c.** Determine the limit: \[ \lim_{x \to \infty} \frac{3}{5 + 2^x} \] This expression seeks the limit of \(\frac{3}{5 + 2^x}\) as \(x\) goes to infinity. ### Explanation - **Summation (\(\Sigma\))**: Summation is a concise way of adding a sequence of numbers, and it’s particularly useful when dealing with series. - **Limit (\(\lim\))**: A limit describes the value that a function approaches as the input (or index) approaches some value. It's a fundamental concept in calculus, particularly useful in defining continuity, derivatives, and integrals. These mathematical processes are fundamental for solving various problems in calculus and analysis, providing tools for understanding change, growth, and complex series. ---
Transcribed Image Text:Certainly! Here’s a transcription and explanation suitable for an educational website: --- ### Mathematical Expressions **a.** Evaluate the summation: \[ \sum_{i=1}^{4} \frac{2}{i + 1} \] This expression represents the sum of terms where each term is calculated as \(\frac{2}{i + 1}\), with the index \(i\) ranging from 1 to 4. **b.** Calculate the limit: \[ \lim_{x \to \infty} \frac{3}{5 + 2^{-x}} \] Here, the expression asks for the limit of the fraction \(\frac{3}{5 + 2^{-x}}\) as \(x\) approaches infinity. **c.** Determine the limit: \[ \lim_{x \to \infty} \frac{3}{5 + 2^x} \] This expression seeks the limit of \(\frac{3}{5 + 2^x}\) as \(x\) goes to infinity. ### Explanation - **Summation (\(\Sigma\))**: Summation is a concise way of adding a sequence of numbers, and it’s particularly useful when dealing with series. - **Limit (\(\lim\))**: A limit describes the value that a function approaches as the input (or index) approaches some value. It's a fundamental concept in calculus, particularly useful in defining continuity, derivatives, and integrals. These mathematical processes are fundamental for solving various problems in calculus and analysis, providing tools for understanding change, growth, and complex series. ---
Expert Solution
Step 1

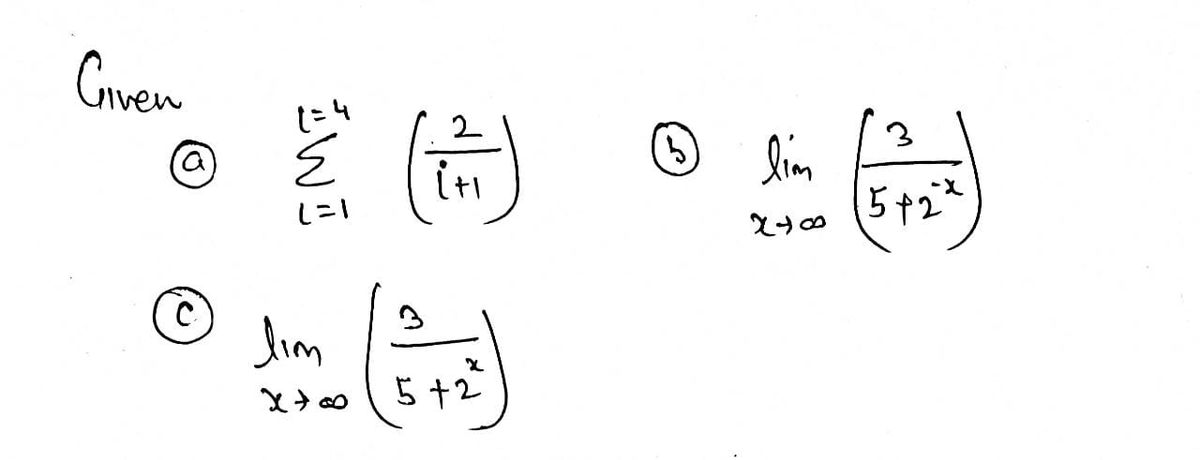
Calculus homework question answer, step 1, image 1

steps

Step by step

Solved in 2 steps with 2 images

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer
Recommended textbooks for you
Calculus: Early Transcendentals
Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning
Thomas' Calculus (14th Edition)
Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON
Calculus: Early Transcendentals (3rd Edition)
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON
Calculus: Early Transcendentals
Calculus: Early Transcendentals
Calculus
ISBN:
9781319050740
Author:
Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:
W. H. Freeman
Precalculus
Precalculus
Calculus
ISBN:
9780135189405
Author:
Michael Sullivan
Publisher:
PEARSON
Calculus: Early Transcendental Functions
Calculus: Early Transcendental Functions
Calculus
ISBN:
9781337552516
Author:
Ron Larson, Bruce H. Edwards
Publisher:
Cengage Learning
SEE MORE TEXTBOOKS