a)-What is fof g ofh 3)? fari= gal= bprove f:R¬R fer )=4lis not Surgective and is not injective.
a)-What is fof g ofh 3)? fari= gal= bprove f:R¬R fer )=4lis not Surgective and is not injective.
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
![**Mathematics Practice Problems**
**a) Problem:**
Calculate the value of \( f(g(h(3))) \).
Given functions:
- \( f(x) = 2^x \)
- \( g(x) = x^2 \)
- \( h(x) = \frac{x}{4} \)
**b) Problem:**
Prove that the function \( f: \mathbb{R} \rightarrow \mathbb{R} \) defined by \( f(x) = |x| \) is not surjective and is not injective.
---
**Solutions:**
**a) Solution:**
1. **Find \( h(3) \):**
\[
h(3) = \frac{3}{4}
\]
2. **Find \( g(h(3)) \):**
\[
g\left(\frac{3}{4}\right) = \left(\frac{3}{4}\right)^2 = \frac{9}{16}
\]
3. **Find \( f(g(h(3))) \):**
\[
f\left(\frac{9}{16}\right) = 2^{\frac{9}{16}}
\]
**b) Solution:**
*To prove \( f: \mathbb{R} \to \mathbb{R} \), \( f(x) = |x| \) is not surjective:*
- A function is surjective if for every \( y \) in the codomain, there is an \( x \) in the domain such that \( f(x) = y \).
- The codomain is \(\mathbb{R}\), but \( f(x) = |x| \) only outputs non-negative values. Therefore, negative numbers in \(\mathbb{R}\) have no pre-image under \( f \).
- Thus, \( f \) is not surjective.
*To prove \( f: \mathbb{R} \to \mathbb{R} \), \( f(x) = |x| \) is not injective:*
- A function is injective if \( f(x_1) = f(x_2) \) implies \( x_1 = x_2 \).
- For instance, \( f(1) = 1 \) and \( f(-1) = 1 \), so](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F39c6e25e-d467-4ba4-a648-1f12925c88db%2F4f8591b9-7878-48e6-a9b2-be9a4e080ed5%2Fadzzaet.jpeg&w=3840&q=75)
Transcribed Image Text:**Mathematics Practice Problems**
**a) Problem:**
Calculate the value of \( f(g(h(3))) \).
Given functions:
- \( f(x) = 2^x \)
- \( g(x) = x^2 \)
- \( h(x) = \frac{x}{4} \)
**b) Problem:**
Prove that the function \( f: \mathbb{R} \rightarrow \mathbb{R} \) defined by \( f(x) = |x| \) is not surjective and is not injective.
---
**Solutions:**
**a) Solution:**
1. **Find \( h(3) \):**
\[
h(3) = \frac{3}{4}
\]
2. **Find \( g(h(3)) \):**
\[
g\left(\frac{3}{4}\right) = \left(\frac{3}{4}\right)^2 = \frac{9}{16}
\]
3. **Find \( f(g(h(3))) \):**
\[
f\left(\frac{9}{16}\right) = 2^{\frac{9}{16}}
\]
**b) Solution:**
*To prove \( f: \mathbb{R} \to \mathbb{R} \), \( f(x) = |x| \) is not surjective:*
- A function is surjective if for every \( y \) in the codomain, there is an \( x \) in the domain such that \( f(x) = y \).
- The codomain is \(\mathbb{R}\), but \( f(x) = |x| \) only outputs non-negative values. Therefore, negative numbers in \(\mathbb{R}\) have no pre-image under \( f \).
- Thus, \( f \) is not surjective.
*To prove \( f: \mathbb{R} \to \mathbb{R} \), \( f(x) = |x| \) is not injective:*
- A function is injective if \( f(x_1) = f(x_2) \) implies \( x_1 = x_2 \).
- For instance, \( f(1) = 1 \) and \( f(-1) = 1 \), so
Expert Solution
Step 1
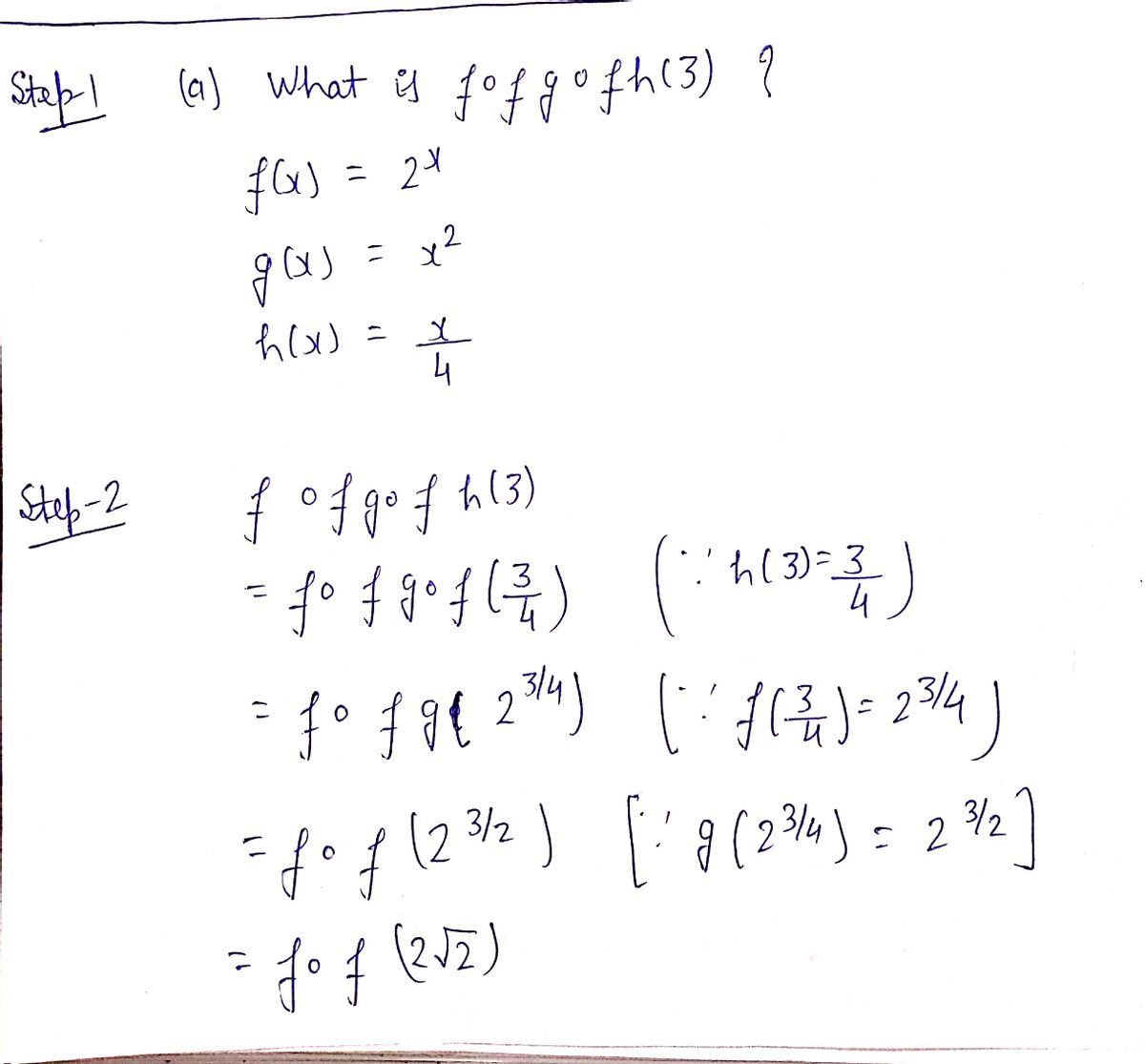
Step by step
Solved in 2 steps with 2 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Similar questions
Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

