(a) What are the mean and standard deviation of the sampling distribution of X? Describe the shape of the sampling distribution of x. We are given that a random sample of size n= 64 is selected from a population with mean = 80 and standard deviation = First, we are asked to determine the mean and standard deviation of the sampling distribution of the sample mean, x. Recall the general properties of the sampling distribution x. The mean is, and the standard deviation is . We can use these formulas to make the desired calculations, rounding a result to three decimal places if it is not exact. Vn a = √64 Submit Skip (you cannot come back)
(a) What are the mean and standard deviation of the sampling distribution of X? Describe the shape of the sampling distribution of x. We are given that a random sample of size n= 64 is selected from a population with mean = 80 and standard deviation = First, we are asked to determine the mean and standard deviation of the sampling distribution of the sample mean, x. Recall the general properties of the sampling distribution x. The mean is, and the standard deviation is . We can use these formulas to make the desired calculations, rounding a result to three decimal places if it is not exact. Vn a = √64 Submit Skip (you cannot come back)
A First Course in Probability (10th Edition)
10th Edition
ISBN:9780134753119
Author:Sheldon Ross
Publisher:Sheldon Ross
Chapter1: Combinatorial Analysis
Section: Chapter Questions
Problem 1.1P: a. How many different 7-place license plates are possible if the first 2 places are for letters and...
Related questions
Question
ANSWER THE BLANK SPACES PLEASE TY!

Transcribed Image Text:Tutorial Exercise
Suppose that a random sample of size 64 is to be selected from a population with mean 80 and standard deviation 10.
(a) What are the mean and standard deviation of the sampling distribution of X? Describe the shape of the sampling distribution of X.
(b) What is the approximate probability that x will be within 0.6 of the population mean u?
(c) What is the approximate probability that x will differ from μ by more than 1.8?
Step 1
(a) What are the mean and standard deviation of the sampling distribution of X? Describe the shape of the sampling distribution of X.
We are given that a random sample of size n = 64 is selected from a population with mean μ = 80 and standard deviation = 10. First, we are asked to determine the mean and standard deviation of the sampling distribution of the sample mean, x.
o
Recall the general properties of the sampling distribution x. The mean is μ = μ, and the standard deviation is σ- =
Vn
μ= = μl
xi
O
√n
√64
Submit Skip (you cannot come back)
We can use these formulas to make the desired calculations, rounding a result to three decimal places if it is not exact.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 2 steps

Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
6. FILL IN THE BLANKS PLEASE TY!
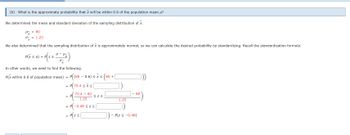
Transcribed Image Text:(b) What is the approximate probability that will be within 0.6 of the population mean μ?
We determined the mean and standard deviation of the sampling distribution of x.
μ = 80
x = 1.25
We also determined that the sampling distribution of x is approximately normal, so we can calculate the desired probability by standardizing. Recall the standardization formula.
a μ-
σ-
In other words, we need to find the following.
P(x within 0.6 of population mean) = P((80-0.6) ≤ x ≤ (80+
= P(79.
P(x ≤ a) = PzS
79.4 ≤x≤
79.4 - 80
1.25
= P(-0.
= P(Z ≤[
≤Z≤
-0.48 ≤z≤
1.25
80
- P(Z < -0.48)
Solution
Recommended textbooks for you

A First Course in Probability (10th Edition)
Probability
ISBN:
9780134753119
Author:
Sheldon Ross
Publisher:
PEARSON


A First Course in Probability (10th Edition)
Probability
ISBN:
9780134753119
Author:
Sheldon Ross
Publisher:
PEARSON
