Homework Help is Here – Start Your Trial Now!
Math
Geometry
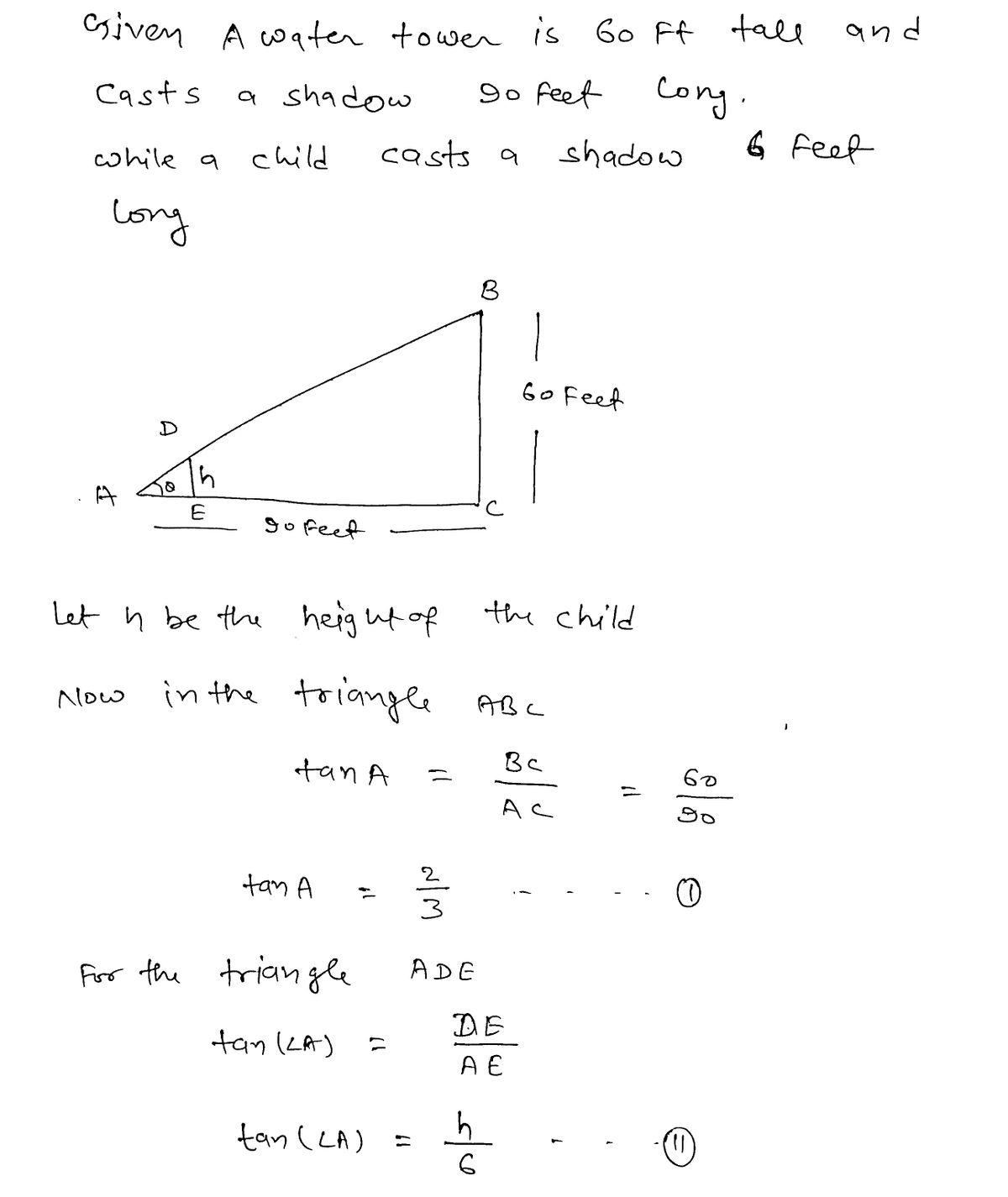
A water tower is 60 feet tall and casts a shadow 90 feet long, while a child casts a shadow 6 feet long. How tall is the child? The child is feet tall. Enter an integer or decimal number [more..]

A water tower is 60 feet tall and casts a shadow 90 feet long, while a child casts a shadow 6 feet long. How tall is the child? The child is feet tall. Enter an integer or decimal number [more..]

Elementary Geometry For College Students, 7e
Elementary Geometry For College Students, 7e
7th Edition
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Alexander, Daniel C.; Koeberlein, Geralyn M.
ChapterP: Preliminary Concepts
SectionP.CT: Test
Problem 1CT
See similar textbooks
icon
Related questions
Question

I crossed multipled and got 9ft it was wrong. How would I solve this problem?

A water tower is 60 feet tall and casts a shadow 90 feet long, while a child casts a shadow 6 feet long. How tall is the child? The child is [ ] feet tall. [Enter an integer or decimal number] Submit Question --- For educational websites, you can explain the problem like this: This problem involves using proportions to find the height of the child. Given that the water tower's height and shadow length are known, you can set up a proportion: \[ \frac{\text{Height of water tower}}{\text{Shadow of water tower}} = \frac{\text{Height of child}}{\text{Shadow of child}} \] Plugging in the known values, you get: \[ \frac{60}{90} = \frac{\text{Height of child}}{6} \] Solving this proportion will give you the height of the child.
Transcribed Image Text:A water tower is 60 feet tall and casts a shadow 90 feet long, while a child casts a shadow 6 feet long. How tall is the child? The child is [ ] feet tall. [Enter an integer or decimal number] Submit Question --- For educational websites, you can explain the problem like this: This problem involves using proportions to find the height of the child. Given that the water tower's height and shadow length are known, you can set up a proportion: \[ \frac{\text{Height of water tower}}{\text{Shadow of water tower}} = \frac{\text{Height of child}}{\text{Shadow of child}} \] Plugging in the known values, you get: \[ \frac{60}{90} = \frac{\text{Height of child}}{6} \] Solving this proportion will give you the height of the child.
Expert Solution
Step 1

Geometry homework question answer, step 1, image 1

steps

Step by step

Solved in 2 steps with 2 images

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer