A toy store would like to open a new store in the city of Thousand Oaks, and they would like to know what proportion of households have kids. Out of 200 households sampled, 124 had kids. Based on this, construct a 95% confidence interval for the true population proportion of Thousand Oaks households with kids. Enter your answer as an open-interval (i.e., parentheses) using decimals (not percents) accurate to three decimal places. Confidence interval = Express the same answer as a tri-linear inequality using decimals (not percents) accurate to three decimal places. < p < Express the same answer using the point estimate and margin of error. Give your answers as decimals, to three places. p = ±
A toy store would like to open a new store in the city of Thousand Oaks, and they would like to know what proportion of households have kids. Out of 200 households sampled, 124 had kids. Based on this, construct a 95% confidence interval for the true population proportion of Thousand Oaks households with kids.
- Enter your answer as an open-interval (i.e., parentheses) using decimals (not percents) accurate to three decimal places.
Confidence interval =
- Express the same answer as a tri-linear inequality using decimals (not percents) accurate to three decimal places. < p <
- Express the same answer using the point estimate and margin of error. Give your answers as decimals, to three places. p = ±
Obtain the 95% confidence interval for the true population proportion of Thousand Oaks households with kids.
The 95% confidence interval for the true population proportion of Thousand Oaks households with kids is obtained below:

Obtain the critical value of z at the 95% confidence level.
Here, confidence level is 0.95.

Use EXCEL Procedure for finding the critical value of z.
Follow the instruction to obtain the critical value of z:
- Open EXCEL
- Go to Formula bar.
- In formula bar enter the function as“=NORMINV”
- Enter the probability as 0.975.
- Enter the mean as 0 and the Standard deviation as 1.
- Click enter
EXCEL output:
From the EXCEL output, the critical value of z at the 95% confidence level is 1.96.
The value of sample proportion is,

The required confidence interval is,
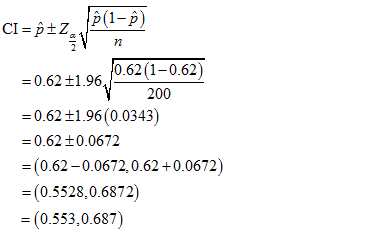

Express the 95% confidence interval for the true population proportion of Thousand Oaks households with kids in the form of tri linear inequality.
The 95% confidence interval for the true population proportion of Thousand Oaks households with kids is expressed in the form of the tri linear inequality as follows:
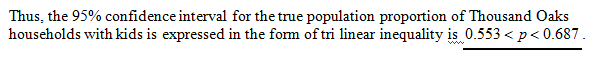
Step by step
Solved in 3 steps with 7 images









