A tank is filled with a fluid with density 54 The cross-section of the end of the tank is given by the shaded region shown below that is bounded by the y-axis, the function written as y= f(x) or x = g(y), and the line y = 12 as shown in the image below. (Note: Assume c = 5 m and d = 12 m.) d +4= f(x) or x= g(y) kg m³ The tank extends back a length of 9 meters as shown in the image below: y=f(x) L { x = g(y) or Ay Basic Vars Funcs Trig Our goal in this problem is to compute the work required pump the liquid 4 meters over the top edge of the tank: X Report the volume, force and work for a slice: Note: Type "Delta x" for Ax or "Delta y" for Ay. Delta must be capitalized. Alternatively, you can put your cursor in the box and when the CalcPad opens select Vars as shown below. Ax Length g(y) f(x)

A tank is filled with a fluid with density 54 kg/m^3

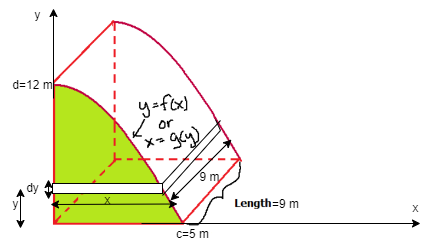
The cross-section of the end of the tank is given by the shaded region shown below that is bounded by the y-axis, the function written as y = f(x) or x = g(y), and the line y = 12 as shown in the image below. (Note: Assume c = 5m and d = 12m.)

(Image 1 see screenshots)

The tank extends back a length of 9 meters as shown in the image below:

(Image 2 see screenshots)

Our goal in this problem is to compute the work required to pump the liquid 4 meters over the top edge of the tank:

Report the volume, force and work for a slice:

Volume of a slice: []

Force for a slice: []

Work for a slice: []

Report the integral for the work. Note: a and b are the lower and upper limits of the integral:

b = []

work = integral [] dy

a = []

Your answer will involve f(x) or g(y) (or possibly both). You will not be able to actually evaluate the integral.

Inlude a drawing with the slice (dimensions labeled) in your work.

Is there a tank of the same size and same basic shape that would require less work to empty? Explain/justify your answer.