country aged 18 and older conducted by a reputable polling organization found that 425 have donated blood in the past two years. Obtain a point estimate for the population proportion of adults in the country aged 18 and older who have donated blood in the past two years. p = (Round to three decimal places as needed
country aged 18 and older conducted by a reputable polling organization found that 425 have donated blood in the past two years. Obtain a point estimate for the population proportion of adults in the country aged 18 and older who have donated blood in the past two years. p = (Round to three decimal places as needed
MATLAB: An Introduction with Applications
6th Edition
ISBN:9781119256830
Author:Amos Gilat
Publisher:Amos Gilat
Chapter1: Starting With Matlab
Section: Chapter Questions
Problem 1P
Related questions
Question
A survey of 2325 adults in a certain large country aged 18 and older conducted by a reputable polling organization found that 425 have donated blood in the past two years.
Obtain a point estimate for the population proportion of adults in the country aged 18 and older who have donated blood in the past two years.
p =
(Round to three decimal places as needed.)

Transcribed Image Text:**Standard Normal Distribution Table**
*Page: 2*
---
**Overview:**
The image contains part of a Standard Normal Distribution Table used for statistical analyses. This table provides cumulative probabilities associated with the standard normal distribution, often used to find the probability that a statistic is observed below, above, or between values on the Z-distribution.
**Graph Explanation:**
In the top-left corner, there is a graphical representation of the standard normal distribution curve. The bell-shaped curve signifies the area under the curve, with a label "Area" showing the cumulative probability to the left of a specified Z-value (denoted by 'z').
**Table Description:**
The table lists Z-scores (standard scores) and their corresponding cumulative probabilities. A Z-score indicates how many standard deviations an element is from the mean of the standard normal distribution.
The table consists of columns and rows:
- The leftmost column represents the Z-score's first decimal place.
- The top row represents the Z-score's second decimal place.
- The body of the table provides cumulative probabilities for each Z-score.
**Example:**
For a Z-score of 0.23, find '0.2' in the leftmost column and '0.03' in the top row. The intersecting cell, 0.5910, is the cumulative probability.
**Z-Score Table:**
| z | 0.00 | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | 0.06 | 0.07 | 0.08 | 0.09 |
|:--------:|:-----:|:-----:|:-----:|:-----:|:-----:|:-----:|:-----:|:-----:|:-----:|:-----:|
| 0.0 | 0.5000 | 0.5040 | 0.5080 | 0.5120 | 0.5160 | 0.5199 | 0.5239 | 0.5279 | 0.5319 | 0.5359 |
| 0.1 | 0.5398 | 0.5438 | 0.5478 | 0.5517 | 0.5557 | 0.5596 |

Transcribed Image Text:**Standard Normal Distribution Table (Page 1)**
**Description:**
This table provides probability values associated with the standard normal distribution, denoted as Z. The standard normal distribution is a continuous probability distribution with a mean of 0 and a standard deviation of 1. It is a special case of the normal distribution.
**Diagram Overview:**
At the top left of the page, there is a bell-shaped curve representing the standard normal distribution. This graph illustrates the symmetry of the distribution, with the area under the curve representing probabilities. The shaded area to the left of a specific value of Z represents the cumulative probability up to that Z-value.
**Table Explanation:**
The table consists of Z-scores ranging from -3.4 to 0.0, with probabilities listed to the right of each Z-score. These probabilities indicate the likelihood of a standard normal random variable being less than or equal to a particular Z-score.
- The first column contains Z values increasing in increments of 0.1.
- The top row includes decimal values ranging from 0.00 to 0.09, which help refine the Z-score lookup.
- The intersection of a Z value and a decimal value provides the cumulative probability for that specific Z-score.
**Example:**
For a Z-score of -1.5, you find the intersection of the row for -1.5 and the column for 0.00, which gives a cumulative probability of 0.0668. If you're looking for the probability of Z being less than or equal to -1.54, find the intersection of the row for -1.5 and the column for 0.04, which is 0.0618.
This table is instrumental in finding probabilities related to the standard normal distribution in statistical analyses and hypothesis testing.
Expert Solution
Step 1: Given information
According to the given information in this question, we are going to find the point estimate by the use of the formula
Step by step
Solved in 3 steps

Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
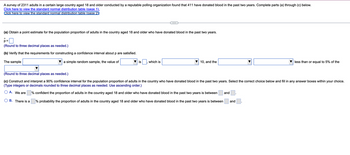
Transcribed Image Text:A survey of 2311 adults in a certain large country aged 18 and older conducted by a reputable polling organization found that 411 have donated blood in the past two years. Complete parts (a) through (c) below.
Click here to view the standard normal distribution table (page 1).
Click here to view the standard normal distribution table (page 2)
(a) Obtain a point estimate for the population proportion of adults in the country aged 18 and older who have donated blood in the past two years.
p=
(Round to three decimal places as needed.)
(b) Verify that the requirements for constructing a confidence interval about p are satisfied.
The sample
a simple random sample, the value of
is which is
B. There is a
10, and the
(Round to three decimal places as needed.)
(c) Construct and interpret a 90% confidence interval for the population proportion of adults in the country who have donated blood in the past two years. Select the correct choice below and fill in any answer boxes within
(Type integers or decimals rounded to three decimal places as needed. Use ascending order.)
O A. We are
% confident the proportion of adults in the country aged 18 and older who have donated blood in the past two years is between and
% probability the proportion of adults in the country aged 18 and older who have donated blood in the past two years is between
less than or equal to 5% of the
and
your
choice.
Solution
Follow-up Question
![A survey of 3,225 adults in a certain large country aged 18 and older conducted by a reputable polling organization found that 425 have donated blood in the past two years. Complete parts (a) through (c) below.
---
(a) Obtain a point estimate for the population proportion of adults in the country aged 18 and older who have donated blood in the past two years.
\(\hat{p} = 0.183\)
(Round to three decimal places as needed.)
(b) Verify that the requirements for constructing a confidence interval about p are satisfied.
The sample [Dropdown] a simple random sample, the value of [Dropdown] is [ ], which is [Dropdown] 10, and the [Dropdown] [Dropdown] [Dropdown] less than or equal to 5% of the [Dropdown].
(Round to three decimal places as needed.)
---
This section is guiding individuals on estimating and verifying conditions for a population proportion based on a specific survey dataset. There are interactive elements such as drop-down menus for selecting the correct statistical terms or values needed to complete part (b) of the question.](https://content.bartleby.com/qna-images/question/ac3be618-b645-4bd8-855b-808ff3fc18d4/b1d61920-2a77-4a22-8913-1c4ca340367a/stu7ohi_thumbnail.png)
Transcribed Image Text:A survey of 3,225 adults in a certain large country aged 18 and older conducted by a reputable polling organization found that 425 have donated blood in the past two years. Complete parts (a) through (c) below.
---
(a) Obtain a point estimate for the population proportion of adults in the country aged 18 and older who have donated blood in the past two years.
\(\hat{p} = 0.183\)
(Round to three decimal places as needed.)
(b) Verify that the requirements for constructing a confidence interval about p are satisfied.
The sample [Dropdown] a simple random sample, the value of [Dropdown] is [ ], which is [Dropdown] 10, and the [Dropdown] [Dropdown] [Dropdown] less than or equal to 5% of the [Dropdown].
(Round to three decimal places as needed.)
---
This section is guiding individuals on estimating and verifying conditions for a population proportion based on a specific survey dataset. There are interactive elements such as drop-down menus for selecting the correct statistical terms or values needed to complete part (b) of the question.
Solution
Recommended textbooks for you

MATLAB: An Introduction with Applications
Statistics
ISBN:
9781119256830
Author:
Amos Gilat
Publisher:
John Wiley & Sons Inc

Probability and Statistics for Engineering and th…
Statistics
ISBN:
9781305251809
Author:
Jay L. Devore
Publisher:
Cengage Learning

Statistics for The Behavioral Sciences (MindTap C…
Statistics
ISBN:
9781305504912
Author:
Frederick J Gravetter, Larry B. Wallnau
Publisher:
Cengage Learning

MATLAB: An Introduction with Applications
Statistics
ISBN:
9781119256830
Author:
Amos Gilat
Publisher:
John Wiley & Sons Inc

Probability and Statistics for Engineering and th…
Statistics
ISBN:
9781305251809
Author:
Jay L. Devore
Publisher:
Cengage Learning

Statistics for The Behavioral Sciences (MindTap C…
Statistics
ISBN:
9781305504912
Author:
Frederick J Gravetter, Larry B. Wallnau
Publisher:
Cengage Learning

Elementary Statistics: Picturing the World (7th E…
Statistics
ISBN:
9780134683416
Author:
Ron Larson, Betsy Farber
Publisher:
PEARSON

The Basic Practice of Statistics
Statistics
ISBN:
9781319042578
Author:
David S. Moore, William I. Notz, Michael A. Fligner
Publisher:
W. H. Freeman

Introduction to the Practice of Statistics
Statistics
ISBN:
9781319013387
Author:
David S. Moore, George P. McCabe, Bruce A. Craig
Publisher:
W. H. Freeman