Homework Help is Here – Start Your Trial Now!
Math
Statistics
A study found that the mean amount of time cars spent in drive-throughs of a certain fast-food restaurant was 138.7 seconds. Assuming drive-through times are normally distributed with a standard deviation of 31 seconds, complete parts (a) through (d) below. Click here to view the standard normal distribution table (page 1). Click here to view the standard normal distribution table (page 2). (a) What is the probability that a randomly selected car will get through the restaurant's drive-through in less than 103 seconds? The probability that a randomly selected car will get through the restaurant's drive-through in less than 103 seconds is 0.1251. (Round to four decimal places as needed.) (b) What is the probability that a randomly selected car will spend more than 191 seconds in the restaurant's drive-through? The probability that a randomly selected car will spend more than 191 seconds in the restaurant's drive-through is (Round to four decimal places as needed.)

A study found that the mean amount of time cars spent in drive-throughs of a certain fast-food restaurant was 138.7 seconds. Assuming drive-through times are normally distributed with a standard deviation of 31 seconds, complete parts (a) through (d) below. Click here to view the standard normal distribution table (page 1). Click here to view the standard normal distribution table (page 2). (a) What is the probability that a randomly selected car will get through the restaurant's drive-through in less than 103 seconds? The probability that a randomly selected car will get through the restaurant's drive-through in less than 103 seconds is 0.1251. (Round to four decimal places as needed.) (b) What is the probability that a randomly selected car will spend more than 191 seconds in the restaurant's drive-through? The probability that a randomly selected car will spend more than 191 seconds in the restaurant's drive-through is (Round to four decimal places as needed.)

Glencoe Algebra 1, Student Edition, 9780079039897, 0079039898, 2018
Glencoe Algebra 1, Student Edition, 9780079039897, 0079039898, 2018
18th Edition
ISBN:9780079039897
Author:Carter
Publisher:Carter
Chapter10: Statistics
Section10.4: Distributions Of Data
Problem 19PFA
See similar textbooks
icon
Related questions
Question
100%
A study found that the mean amount of time cars spent in drive-throughs of a certain fast-food restaurant was 138.7 seconds. Assuming drive-through times are normally distributed with a standard deviation of 31 seconds, complete parts (a) through (d) below. Click here to view the standard normal distribution table (page 1). Click here to view the standard normal distribution table (page 2). (a) What is the probability that a randomly selected car will get through the restaurant's drive-through in less than 103 seconds? The probability that a randomly selected car will get through the restaurant's drive-through in less than 103 seconds is 0.1251. (Round to four decimal places as needed.) (b) What is the probability that a randomly selected car will spend more than 191 seconds in the restaurant's drive-through? The probability that a randomly selected car will spend more than 191 seconds in the restaurant's drive-through is (Round to four decimal places as needed.)
Transcribed Image Text:A study found that the mean amount of time cars spent in drive-throughs of a certain fast-food restaurant was 138.7 seconds. Assuming drive-through times are normally distributed with a standard deviation of 31 seconds, complete parts (a) through (d) below. Click here to view the standard normal distribution table (page 1). Click here to view the standard normal distribution table (page 2). 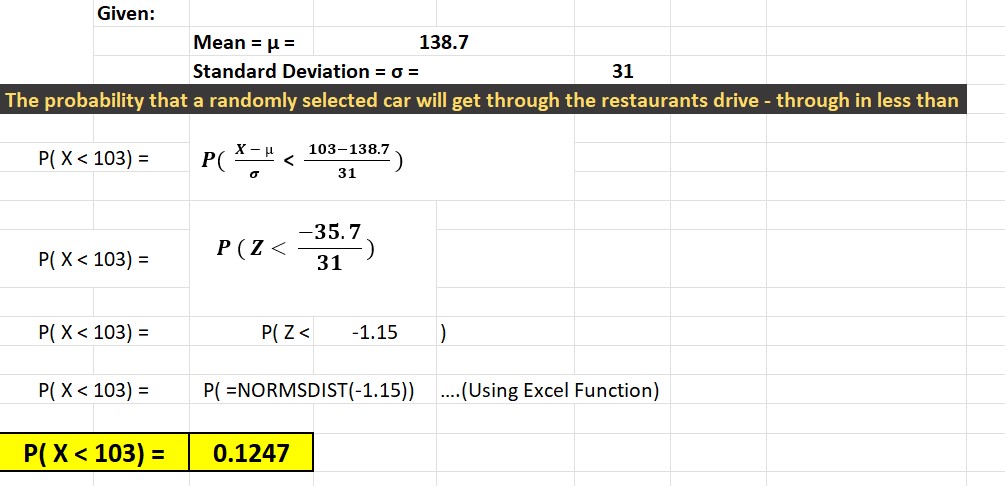(a) What is the probability that a randomly selected car will get through the restaurant's drive-through in less than 103 seconds? The probability that a randomly selected car will get through the restaurant's drive-through in less than 103 seconds is 0.1251. (Round to four decimal places as needed.) (b) What is the probability that a randomly selected car will spend more than 191 seconds in the restaurant's drive-through? The probability that a randomly selected car will spend more than 191 seconds in the restaurant's drive-through is (Round to four decimal places as needed.)
Expert Solution
Step 1

a)

Statistics homework question answer, step 1, image 1

trending now

Trending now

This is a popular solution!

steps

Step by step

Solved in 2 steps with 2 images

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer
Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
A study found that the mean amount of time cars spent in drive-throughs of a certain fast-food restaurant was 138.7 seconds. Assuming drive-through times are normally distributed with a standard deviation of 31 seconds, complete part (a) through (d) below. Click here to view the standard normal distribution table (page 1). Click here to view the standard normal distribution table (page 2). (a) What is the probability that a randomly selected car will get through the restaurant's drive-through in less than 103 seconds? The probability that a randomly selected car will get through the restaurant's drive-through in less than 103 seconds is 0.1251. (Round to four decimal places as needed.) (b) What is the probability that a randomly selected car will spend more than 191 seconds in the restaurant's drive-through? The probability that a randomly selected car will spend more than 191 seconds in the restaurant's drive-through is 0.0458. (Round to four decimal places as needed.) (c) What proportion of cars spend between 2 and 3 minutes in the restaurant's drive-through? The proportion of cars that spend between 2 and 3 minutes in the restaurant's drive-through is. (Round to four decimal places as needed.)
Transcribed Image Text:A study found that the mean amount of time cars spent in drive-throughs of a certain fast-food restaurant was 138.7 seconds. Assuming drive-through times are normally distributed with a standard deviation of 31 seconds, complete part (a) through (d) below. Click here to view the standard normal distribution table (page 1). Click here to view the standard normal distribution table (page 2). (a) What is the probability that a randomly selected car will get through the restaurant's drive-through in less than 103 seconds? The probability that a randomly selected car will get through the restaurant's drive-through in less than 103 seconds is 0.1251. (Round to four decimal places as needed.) (b) What is the probability that a randomly selected car will spend more than 191 seconds in the restaurant's drive-through? The probability that a randomly selected car will spend more than 191 seconds in the restaurant's drive-through is 0.0458. (Round to four decimal places as needed.) (c) What proportion of cars spend between 2 and 3 minutes in the restaurant's drive-through? The proportion of cars that spend between 2 and 3 minutes in the restaurant's drive-through is. (Round to four decimal places as needed.)
Solution
Bartleby Expert
SEE SOLUTION
Recommended textbooks for you
Glencoe Algebra 1, Student Edition, 9780079039897…
Glencoe Algebra 1, Student Edition, 9780079039897…
Algebra
ISBN:
9780079039897
Author:
Carter
Publisher:
McGraw Hill
SEE MORE TEXTBOOKS