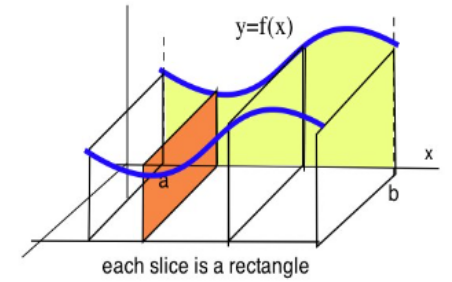
A solid is contructed so that one side is the region between the lines 2 = a, x= =b, the graph of y = f(x) and the x-axis, and the cross- sections of the solid perpendicular to the x-axis are rectangles with base 4 (as shown in the figure). Which of the following integrals represents the volume of this solid? [*4(f(x))² da of 47(f(x))² da of 4 f(a) de S* n(ƒ(2))² da y=f(x) each slice is a rectangle
A solid is contructed so that one side is the region between the lines 2 = a, x= =b, the graph of y = f(x) and the x-axis, and the cross- sections of the solid perpendicular to the x-axis are rectangles with base 4 (as shown in the figure). Which of the following integrals represents the volume of this solid? [*4(f(x))² da of 47(f(x))² da of 4 f(a) de S* n(ƒ(2))² da y=f(x) each slice is a rectangle
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question

Transcribed Image Text:A solid is constructed so that one side is the region between the lines \( x = a \), \( x = b \), the graph of \( y = f(x) \) and the x-axis, and the cross-sections of the solid perpendicular to the x-axis are rectangles with base 4 (as shown in the figure).
Which of the following integrals represents the volume of this solid?
- \(\int_a^b 4(f(x))^2 \, dx\)
- \(\int_a^b 4\pi(f(x))^2 \, dx\)
- \(\int_a^b 4f(x) \, dx\)
- \(\int_a^b \pi(f(x))^2 \, dx\)
**Diagram Explanation:**
The diagram illustrates a three-dimensional solid where the base is bounded by vertical lines at \( x = a \) and \( x = b \), and by the curve \( y = f(x) \) along with the x-axis. The cross-sections perpendicular to the x-axis form rectangles, each with a constant base of 4 units. The height of each rectangle is defined by the value of \( f(x) \) at that point, as depicted by a wave-like blue curve. The volume is calculated by integrating these rectangular cross-sections along the x-axis from \( a \) to \( b \).
Expert Solution
Step 1: Introduction to given details
The given data is:
Step by step
Solved in 3 steps with 3 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

