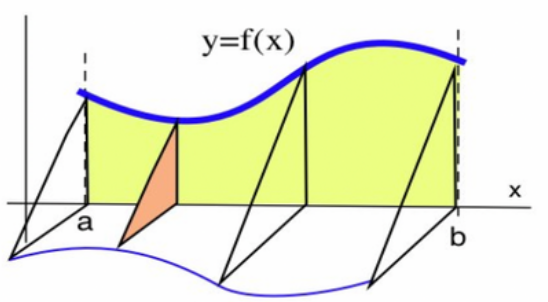
A solid is constructed so that one side is the region between the lines $ x = a $, $ x = b $, the graph of $ y = f(x) $, and the x-axis. The cross-sections of the solid perpendicular to the x-axis are isosceles right triangles, as shown in the figure.**Which of the following integrals represents the volume of this solid?**- $\int_{a}^{b} \pi (f(x))^2 \, dx$- $\int_{a}^{b} \pi (f(x)) \, dx$- $\int_{a}^{b} (f(x))^2 \, dx$- $\int_{a}^{b} \frac{1}{2}(f(x))^2 \, dx$**Diagram Explanation:**The diagram illustrates the solid, where the region under the curve $ y = f(x) $ between $ x = a $ and $ x = b $ forms one side of the solid. Each slice perpendicular to the x-axis is shown as an isosceles right triangle, with the base and height equal to the value of $ f(x) $ at that slice. The volume of the solid is determined by integrating the area of these triangular slices along the interval $[a, b]$.

A solid is constructed so that one side is the region between the lines 0, 1= b, the graph of y = f(x) and the x-axis, and the cross- sections of the solid perpendicular to the x-axis are isosceles right triangles, as shown in the figure. Which of the following integrals represents the volume of this solid? S* n(f(x))² dæ b T(f(x)) dr [- f(f(=))² dz 4 Ba ½ (12))²2 de da y=f(x) each slice is a right triangle with base = height

A solid is constructed so that one side is the region between the lines 0, 1= b, the graph of y = f(x) and the x-axis, and the cross- sections of the solid perpendicular to the x-axis are isosceles right triangles, as shown in the figure. Which of the following integrals represents the volume of this solid? S* n(f(x))² dæ b T(f(x)) dr [- f(f(=))² dz 4 Ba ½ (12))²2 de da y=f(x) each slice is a right triangle with base = height

Advanced Engineering Mathematics

10th Edition

ISBN:9780470458365

Author:Erwin Kreyszig

Publisher:Erwin Kreyszig

Chapter2: Second-order Linear Odes

Section: Chapter Questions

Problem 1RQ

See similar textbooks

Similar questions

A snack company is preparing two mixtures of snacks from a supply of 110 pounds pretzels, 30 pounds pistachios, 10 pounds cheese puffs, 60 pounds sesame sticks, and 20 pounds toffee bites. Mixture X contains 55% pretzels, 20% pistachios, 5% cheese puffs, 20% sesame sticks, and no toffee bites, and sells for $7.99 per pound. Mixture Y contains 45% pretzels, 10% pistachios, no cheese puffs, 10 % sesame sticks, and 15% toffee bites, and sells for $5.99 per pound. If x = # of pounds of Snack X and y = # of pounds of Snack Y, determine the constraints on this linear programming problem. Inequality for pretzels [ Choose ] Inequality for pistachios ( Choose] Inequality for cheese puffs ( Choose ) Inequality for sesame sticks [Choose ] Inequality for toffee bits [ Choose ) Non-negativity inequalities [ Choose ] >
Find the area of the region bounded on the left by the curves y = e and y = 3-2, and on the right by the line r = 1. (a) (e –1) 2 (e* – 1) – 3 In 3 2 1 (c) In 3 1 2e3 (d) 3 In 3 1. 3 1 (e) 3 In 3
3. [А the graph of y = x3, on the interval [0, 1], is revolved about the Find the surface area of the volume generated when у-аxis.
Find the volume of the solid in revolution as it rotates about the axis and the function 1. f(x) = x(2 – x) 0
7) The region bounded by y= √x, y= 2, x=0 is revolved about the y-axis to generate a solid, its volume is: (23/5)pi C. units. (32/5)pi C. units. (5/23)pi C. units. (5/32)pi C. units.
Let R be the region enclosed by the graphs of g(x) = -2+3 cos (x) and h(x) = 6 - 2(x - 1)², the y-axis, and the line x = 2, as shown in the figure to the right. 1. Find the volume of the solid generated when R is rotated about the horizontal line y = 6. 2. Region R is the base of a solid. For this solid, each cross section perpendicular to the x-axis is a square. Find the volume of the solid. 3. Region R is the base of a solid. For this solid, each cross section perpendicular to the x-axis has area A(x) = Find the volume of the solid. 2x²43