A solid cube of side c= 120 mm is attached as shown to a cord AB of length 240 mm. The cube spins about its diagonal BC and precesses about the vertical axis AD Knowing that 0= 25° and β= 40°, determine (a) the rate of spin of the cube, (b) its rate of precession. (See hint of Prob. 18.115.)
A solid cube of side c= 120 mm is attached as shown to a cord AB of length 240 mm. The cube spins about its diagonal BC and precesses about the vertical axis AD Knowing that 0= 25° and β= 40°, determine (a) the rate of spin of the cube, (b) its rate of precession. (See hint of Prob. 18.115.)
Draw the free body diagram of the system.
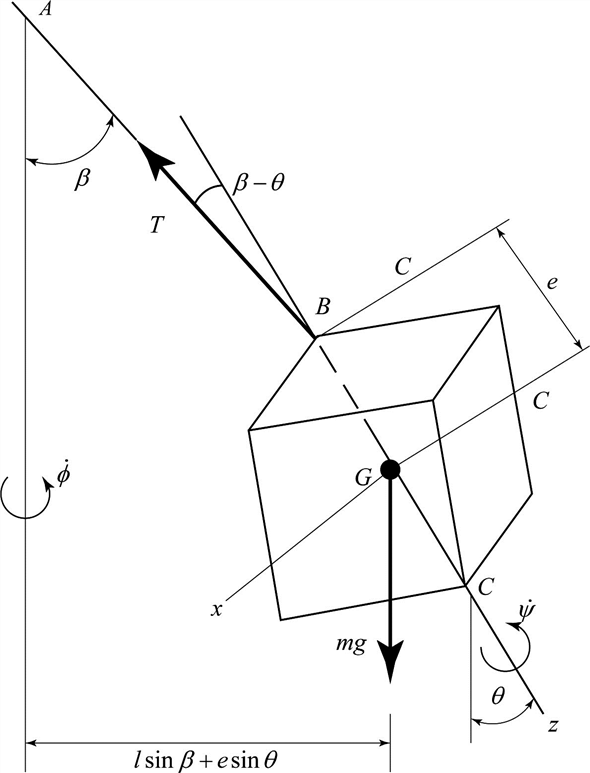
The axes are taken in such a way that z axis passes through the diagonal of the body BC and x axis lies in the plane of A, B, C, and D.
G is the center of gravity of the cube and the length of GB is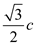 
.
Express the moment of inertia of the cube in x direction:
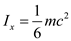
Here, moment of inertia of the cube in x direction is 
, mass is m, and side of the cube is a.
The moment of inertia in x, y, and z directions for a cube is the same.
The moment of inertia in the y and z directions is equal to 
.
Express the angular velocity of the system:
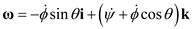…… (1)
Here, angular velocity of the system is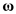 
, rate of precession is 
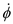, rate of spin is 
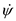, and rate of nutation is 
.
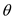Express the angular momentum about the mass center G as:
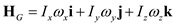
Here, angular momentum about the mass center is G, angular velocity in x direction is
, angular velocity in y direction is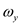 
, and angular velocity in z direction is 
.
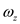Substitute 
for 
, 0 for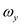 
, and 
for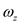 
.
Express the angular velocity of the reference frame Gxyz as:
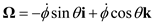
Here, angular velocity for the frame of reference is Gxyz
Express the rate of change of angular momentum:
Here, rate of change of angular momentum is 
and angular momentum about the frame of reference Gxyz is 
Angular momentum about the frame of reference Gxyz is 0.
Substitute 0 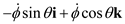for 
, 
for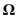 
, and 
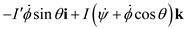for 
.
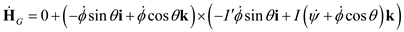…… (2)
Express the vector multiplication:
…… (3)
Substitute Equation (3) in (2).
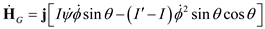
Express the acceleration of the mass center as:
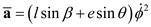…… (4)
Here, acceleration of the mass center is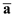 
, length of AB is l, angle is 
, e is the length of GB.
Forces in the upward direction are positive.
Apply moment equilibrium condition for the vertical forces in the free body diagram.
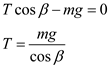…… (5)
Step by step
Solved in 9 steps with 64 images
