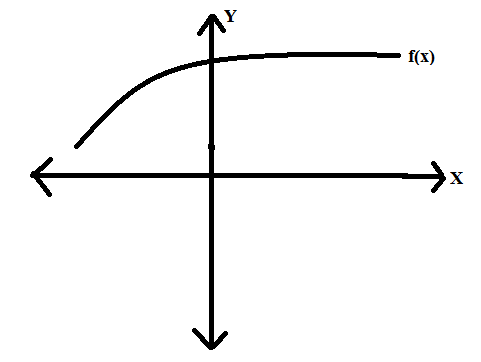
a) Sketch the graph of a function f for which f(x)>0 and f'(x)>0 for all x. b) Sketch the graph of a function g for which g(x)>0 and g'(x)<0 for all x. c) Give formulog f.
Unitary Method
The word “unitary” comes from the word “unit”, which means a single and complete entity. In this method, we find the value of a unit product from the given number of products, and then we solve for the other number of products.
Speed, Time, and Distance
Imagine you and 3 of your friends are planning to go to the playground at 6 in the evening. Your house is one mile away from the playground and one of your friends named Jim must start at 5 pm to reach the playground by walk. The other two friends are 3 miles away.
Profit and Loss
The amount earned or lost on the sale of one or more items is referred to as the profit or loss on that item.
Units and Measurements
Measurements and comparisons are the foundation of science and engineering. We, therefore, need rules that tell us how things are measured and compared. For these measurements and comparisons, we perform certain experiments, and we will need the experiments to set up the devices.
Number 9
![**Educational Website Content**
---
### Understanding Derivatives and Critical Points
**Exercise 5-7**
- **5.** \( f(x) = \frac{2}{3}x^3 - x^2 \)
- **7a.** On the basis of your answers to Exercises 1–6, describe how the first derivative of a function could be used to determine whether a local maximum or a local minimum occurs at a critical number.
- **7b.** If \( c \) is a critical number, is it true that \( (c, f(c)) \) is either a local maximum or minimum point?
---
### Graph Analysis
**8.** The graph of a function \( f \) is shown below with several points labeled.
#### Diagram Explained:
- **Graph Description:** A curve with labeled points A, B, C, and D.
**Questions:**
- **8a.** At which labeled points is \( f' \) positive? Explain.
- **8b.** Between which pairs of labeled points does \( f \) have a critical point?
- **8c.** Between which pairs of labeled points is \( f' \) increasing?
- **8d.** Between which pairs of labeled points does \( f' \) achieve its minimum value?
---
### Graph Sketching
**9.**
- **9a.** Sketch the graph of a function \( f \) for which \( f(x) > 0 \) and \( f'(x) > 0 \) for all \( x \).
- **9b.** Sketch the graph of a function \( g \) for which \( g(x) > 0 \) and \( g'(x) < 0 \) for all \( x \).
- **9c.** Give formulas for functions with these properties.
---
### Numerical Derivatives
**10.** The numerical derivative \( \text{nDeriv} \) frequently calculates misleading values at critical numbers where the derivative is undefined. For example, let \( f(x) = \sqrt[3]{x - 2} \) and \( g(x) = \sqrt[3]{(x - 2)^2} \).
- **Example Explained:**
- At \( x = 2 \), both \( f'(2) \) and \( g'(2) \) do not exist.
-](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F0d5a9cae-3c86-4153-9ed8-d2e45fd1e238%2F28170f71-d4d9-4674-a8f8-fdd8380d1f42%2Fo9s37f.jpeg&w=3840&q=75)
If we have to draw the graph of a function of a differentiable function then it must be continuous
f(x)>0 means that the function is positive for all the values of x the graph would be in 1st and 2nd quadrants but above the x-axis as the graph is positive
f'(x)>0 means that the slope is positive which in turn makes the graph to be increasing as x increases
therefore the graph would be
Step by step
Solved in 2 steps with 2 images









