A similarity transformation that maps one circle onto another must include a rotation. [ Select ] All circles are similar. [Select ] There is always a similarity transformation that will map one circle onto another. [ Select ]
Select whether each statement is true or false.
![Select whether each statement is true or false.
A similarity transformation that maps one circle onto another must include a rotation.
[ Select ]
All circles are similar. [Select ]
There is always a similarity transformation that will map one circle onto another. [Select ]](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F646c3bf8-5b49-43fd-9253-10c21c8cba36%2F882dc289-6965-4c10-beab-cee92006474c%2Fjp5dula_processed.png&w=3840&q=75)
The similarity transformation is a transformation obtained by one or more rigid transformations followed by dilation.
Those rigid transformations may include rotation as well.
Consider the following example of squares:
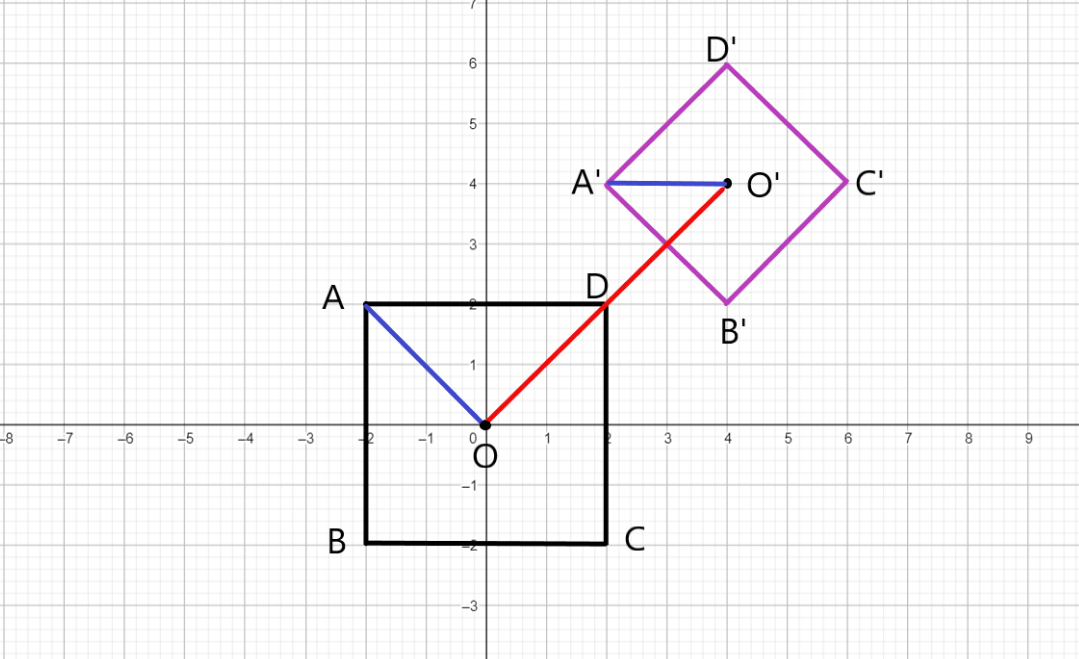
Note that here the square ABCD can be transformed to A'B'C'D' by the following steps:
Translate center O to O'. Now, translate all points along OO'. Then, rotate by and finally dilate by a factor of . Observe that the obtained square is similar to the original square ABCD.
But consider two circles as follows:
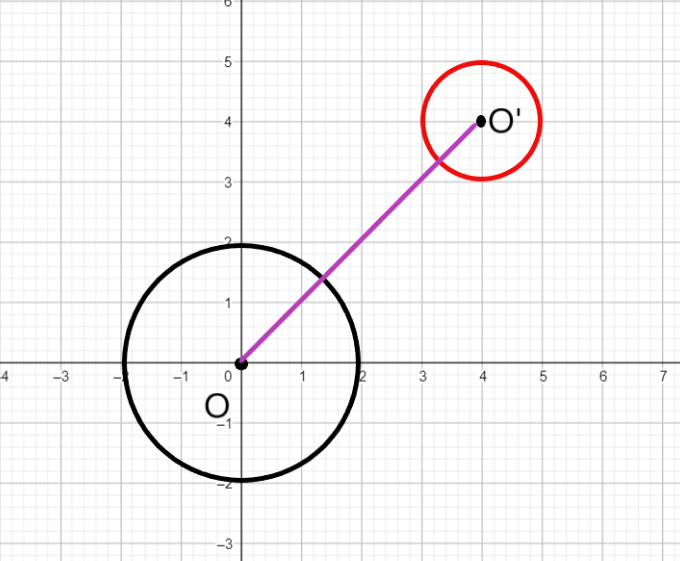
Here, we just need to translate the center O to point O', then, translate all points along OO' and finally dilate according to the ratio of radii.
Thus, for similarity transformation of circles rotation is not necessary. Also, any circle can be transformed into another circle using similarity transformation.
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 2 images




