A recent report by the MLB shows that a typical family of four spends $490 to watch a professional game. Assume the distribution of attending a game in person follows the normal distribution with a mean of $490 and a standard deviation of $30. 1) What is the probability that a randomly selected family of four spends less than $430 to watch a game in person? 2) What is the probability that a randomly selected family of four spends more than $430 to watch a game in person? 3) What is the probability that a randomly selected family of four spends between $430 and $550 to watch a game in person?
A recent report by the MLB shows that a typical family of four spends $490 to watch a professional game. Assume the distribution of attending a game in person follows the
1) What is the
2) What is the probability that a randomly selected family of four spends more than $430 to watch a game in person?
3) What is the probability that a randomly selected family of four spends between $430 and $550 to watch a game in person?
Given Information:
Let the random variable X denotes the attending a game in person.
X has normal distribution with a mean of $490 and a standard deviation of $30.
Hence,
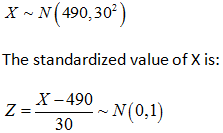
1)
The probability that a randomly selected family of four spends less than $430 to watch a game in person can be obtained as:
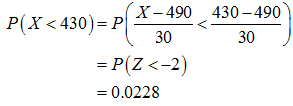
The z-value is obtained using the statistical tables.
Therefore, the probability that a randomly selected family of four spends less than $430 to watch a game in person is 0.0228.
Step by step
Solved in 4 steps with 4 images









