A product is introduced to the market. The weekly profit (in dollars) of that product decays exponentially as function of the price that is charged (in dollars) and is given by P(x) = 85000 · e-0.04.x Suppose the price in dollars of that product, ä(t), changes over time t (in weeks) as given by x(t) = 49 +0.81 · t² Find the rate that profit changes as a function of time, P'(t) How fast is profit changing with respect to time 4 weeks after the introduction. dollars/week dollars/week
A product is introduced to the market. The weekly profit (in dollars) of that product decays exponentially as function of the price that is charged (in dollars) and is given by P(x) = 85000 · e-0.04.x Suppose the price in dollars of that product, ä(t), changes over time t (in weeks) as given by x(t) = 49 +0.81 · t² Find the rate that profit changes as a function of time, P'(t) How fast is profit changing with respect to time 4 weeks after the introduction. dollars/week dollars/week
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
A product is introduced to the market. The weekly profit (in dollars) of that product decays exponentially as function of the price that is charged (in dollars) and is given by �(�)=85000⋅�-0.04⋅�
Suppose the price in dollars of that product, �(�), changes over time � (in weeks) as given by �(�)=49+0.81⋅�2
Find the rate that profit changes as a function of time, �′(�) dollars/week
How fast is profit changing with respect to time 4 weeks after the introduction. dollars/week

Transcribed Image Text:A product is introduced to the market. The weekly profit (in dollars) of that product decays exponentially
as function of the price that is charged (in dollars) and is given by P(x) = 85000.e-0.04.
Suppose the price in dollars of that product, ä(t), changes over time t (in weeks) as given by
x(t) = 49 +0.81 · t²
Find the rate that profit changes as a function of time, P'(t)
How fast is profit changing with respect to time 4 weeks after the introduction.
dollars/week
dollars/week
Expert Solution
Step 1
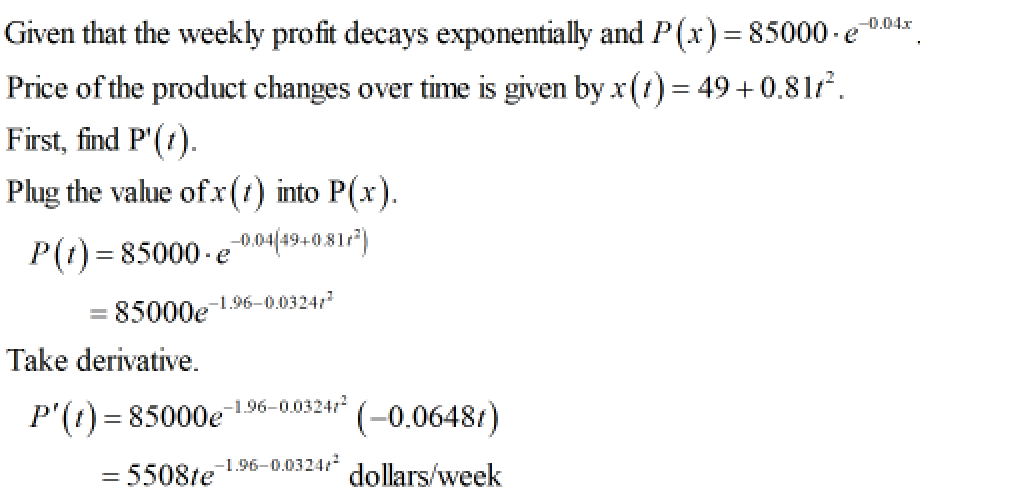
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

