Homework Help is Here – Start Your Trial Now!
Math
Probability
A particular manufacturer (the vendee) uses sample data sent by a vendor to investigate whether the mean length of rods produced by the vendor's production process is truly 10 mm or more, as claimed by the vendor and desired by the vendee. The production process has a standard deviation of 0.03 mm, the vendor supplies n = 200 items to the vendee, and the vendee uses α = .05 in testing Ho: μ = 10 mm against H₂: µ< 10 mm. If the true mean is really μ = 9.9975 mm, what is the chance that they will make a Type II error? What is the probability that the vendee's test will fail to reject the null hypothesis when in fact μ = 9.9975 mm? (Round to four decimal places as needed.)

A particular manufacturer (the vendee) uses sample data sent by a vendor to investigate whether the mean length of rods produced by the vendor's production process is truly 10 mm or more, as claimed by the vendor and desired by the vendee. The production process has a standard deviation of 0.03 mm, the vendor supplies n = 200 items to the vendee, and the vendee uses α = .05 in testing Ho: μ = 10 mm against H₂: µ< 10 mm. If the true mean is really μ = 9.9975 mm, what is the chance that they will make a Type II error? What is the probability that the vendee's test will fail to reject the null hypothesis when in fact μ = 9.9975 mm? (Round to four decimal places as needed.)

A First Course in Probability (10th Edition)
A First Course in Probability (10th Edition)
10th Edition
ISBN:9780134753119
Author:Sheldon Ross
Publisher:Sheldon Ross
Chapter1: Combinatorial Analysis
Section: Chapter Questions
Problem 1.1P: a. How many different 7-place license plates are possible if the first 2 places are for letters and...
See similar textbooks
icon
Related questions
Question

0.1190 is wrong could you please kindly reattempt this?

A particular manufacturer (the vendee) uses sample data sent by a vendor to investigate whether the mean length of rods produced by the vendor's production process is truly 10 mm or more, as claimed by the vendor and desired by the vendee. The production process has a standard deviation of 0.03 mm, the vendor supplies n = 200 items to the vendee, and the vendee uses α = .05 in testing Hỏ: µ = 10 mm against H₂: µ< 10 mm. If the true mean is really μ = 9.9975 mm, what is the chance that they will make a Type Il error? What is the probability that the vendee's test will fail to reject the null hypothesis when in fact μ = 9.9975 mm? (Round to four decimal places as needed.)
Transcribed Image Text:A particular manufacturer (the vendee) uses sample data sent by a vendor to investigate whether the mean length of rods produced by the vendor's production process is truly 10 mm or more, as claimed by the vendor and desired by the vendee. The production process has a standard deviation of 0.03 mm, the vendor supplies n = 200 items to the vendee, and the vendee uses α = .05 in testing Hỏ: µ = 10 mm against H₂: µ< 10 mm. If the true mean is really μ = 9.9975 mm, what is the chance that they will make a Type Il error? What is the probability that the vendee's test will fail to reject the null hypothesis when in fact μ = 9.9975 mm? (Round to four decimal places as needed.)
Expert Solution
trending now

Trending now

This is a popular solution!

steps

Step by step

Solved in 2 steps

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer
Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question

The answer is wrong. Please explain how they got 0.6808.

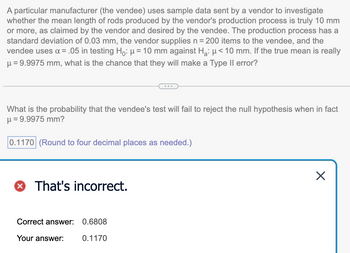
A particular manufacturer (the vendee) uses sample data sent by a vendor to investigate whether the mean length of rods produced by the vendor's production process is truly 10 mm or more, as claimed by the vendor and desired by the vendee. The production process has a standard deviation of 0.03 mm, the vendor supplies n = 200 items to the vendee, and the vendee uses α = .05 in testing Ho: μ = 10 mm against H₂: μ< 10 mm. If the true mean is really μ = 9.9975 mm, what is the chance that they will make a Type II error? What is the probability that the vendee's test will fail to reject the null hypothesis when in fact μ = 9.9975 mm? 0.1170 (Round to four decimal places as needed.) That's incorrect. Correct answer: 0.6808 Your answer: 0.1170 X
Transcribed Image Text:A particular manufacturer (the vendee) uses sample data sent by a vendor to investigate whether the mean length of rods produced by the vendor's production process is truly 10 mm or more, as claimed by the vendor and desired by the vendee. The production process has a standard deviation of 0.03 mm, the vendor supplies n = 200 items to the vendee, and the vendee uses α = .05 in testing Ho: μ = 10 mm against H₂: μ< 10 mm. If the true mean is really μ = 9.9975 mm, what is the chance that they will make a Type II error? What is the probability that the vendee's test will fail to reject the null hypothesis when in fact μ = 9.9975 mm? 0.1170 (Round to four decimal places as needed.) That's incorrect. Correct answer: 0.6808 Your answer: 0.1170 X
Solution
Bartleby Expert
SEE SOLUTION