A mass is attached to a spring, At time t = 0 second, the spring is stretched to a length of 10 cm below its position at rest. The spring is released, and its length 10 seconds later is observed to be 5 cm. Find a formula for the length of the spring at time t seconds.
A mass is attached to a spring, At time t = 0 second, the spring is stretched to a length of 10 cm below its position at rest. The spring is released, and its length 10 seconds later is observed to be 5 cm. Find a formula for the length of the spring at time t seconds.
Given:
A mass is attached to a spring, At time t = 0 second, the spring is stretched to a length of 10 cm below its position at rest. The spring is released, and its length 10 seconds later is observed to be 5 cm.
At the end of the vertical string the mass is attached. The oscillation is mad up and down based on which he mass is pulled downward and it gets released. The laws of physics are applied to this condition.
Based on the Hooke’s law, that defines the string which is being stretched to x-units. The original position is restored by the force F that is directly proportional to the value of x.
It is given by the equation,
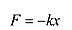
Where k is a positive constant
Newton’s second law of motion states
The force is equal to the product of massand acceleration based on the newton’s second law of motion.

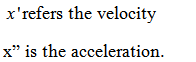
The equation is given as follows,

Here, the value of k and m are positive.
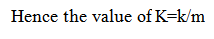

Step by step
Solved in 6 steps with 14 images









