(a) Let A (b) Let A = = x = 1 1 arbitrary mx n matrix and x = = What are the row vectors and column vectors of this matrix? 0 1 1 combination of the column vectors of A, with coefficeints x1, x2, and x3. (c) Now generalize part (b) to the case where A is m x n. That is, show that if A is an X1 X2 and let = . X1 X2 X3 Xn the columns of A, with coefficients x1, x2, Xn. be a vector in R³. Show that Ax is a linear X1 X2 (d) Suppose that A is a 4 x 3 matrix, and let c₁, c2, 3 be the column vectors of A. That is, A [C₁ C₂ C3]. Suppose that E R4 is the vector 6 = 2c₁ - ₂ + 3, and let is in R", then A is a linear combination of Show that A6 is consistent by finding a solution to the system.
(a) Let A (b) Let A = = x = 1 1 arbitrary mx n matrix and x = = What are the row vectors and column vectors of this matrix? 0 1 1 combination of the column vectors of A, with coefficeints x1, x2, and x3. (c) Now generalize part (b) to the case where A is m x n. That is, show that if A is an X1 X2 and let = . X1 X2 X3 Xn the columns of A, with coefficients x1, x2, Xn. be a vector in R³. Show that Ax is a linear X1 X2 (d) Suppose that A is a 4 x 3 matrix, and let c₁, c2, 3 be the column vectors of A. That is, A [C₁ C₂ C3]. Suppose that E R4 is the vector 6 = 2c₁ - ₂ + 3, and let is in R", then A is a linear combination of Show that A6 is consistent by finding a solution to the system.
Elementary Linear Algebra (MindTap Course List)
8th Edition
ISBN:9781305658004
Author:Ron Larson
Publisher:Ron Larson
Chapter3: Determinants
Section3.3: Properties Of Determinants
Problem 63E: Let A be an nn matrix in which the entries of each row sum to zero. Find |A|.
Related questions
Question
![3. (a) Let A =
(b) Let A =
1
1
0
1
1
1
0 1
1 1 1
combination of the column vectors of A, with coefficeints x1, x2, and x3.
(c) Now generalize part (b) to the case where A is m × n. That is, show that if A is an
1 1
0 1 1
1
1
0 1
1 1
18
-
What are the row vectors and column vectors of this matrix?
9
arbitrary mx n matrix and x =
m
and let =
X1
x2
x 3
X1
x2
In
the columns of A, with coefficients x1, x2,., n.
be a vector in R³. Show that A is a linear
2c1
c₂ + c3, and let
(d) Suppose that A is a 4 × 3 matrix, and let c₁, c2, c3 be the column vectors of A. That
A [C₁ C₂ C3]. Suppose that be R4 is the vector 6 = 20₁
[ci
is,
is in R", then A is a linear combination of
9
X1
= X2
. Show that Aỡ = b is consistent by finding a solution to the system.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F293ec77a-bb0f-4498-a317-90c98547c742%2F1afdb19f-7334-4686-a8bc-cfd90415f4a2%2Flflmihj_processed.jpeg&w=3840&q=75)
Transcribed Image Text:3. (a) Let A =
(b) Let A =
1
1
0
1
1
1
0 1
1 1 1
combination of the column vectors of A, with coefficeints x1, x2, and x3.
(c) Now generalize part (b) to the case where A is m × n. That is, show that if A is an
1 1
0 1 1
1
1
0 1
1 1
18
-
What are the row vectors and column vectors of this matrix?
9
arbitrary mx n matrix and x =
m
and let =
X1
x2
x 3
X1
x2
In
the columns of A, with coefficients x1, x2,., n.
be a vector in R³. Show that A is a linear
2c1
c₂ + c3, and let
(d) Suppose that A is a 4 × 3 matrix, and let c₁, c2, c3 be the column vectors of A. That
A [C₁ C₂ C3]. Suppose that be R4 is the vector 6 = 20₁
[ci
is,
is in R", then A is a linear combination of
9
X1
= X2
. Show that Aỡ = b is consistent by finding a solution to the system.
Expert Solution
Step 1
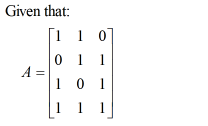
Step by step
Solved in 3 steps with 3 images

Recommended textbooks for you

Elementary Linear Algebra (MindTap Course List)
Algebra
ISBN:
9781305658004
Author:
Ron Larson
Publisher:
Cengage Learning

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage


Elementary Linear Algebra (MindTap Course List)
Algebra
ISBN:
9781305658004
Author:
Ron Larson
Publisher:
Cengage Learning

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage


College Algebra (MindTap Course List)
Algebra
ISBN:
9781305652231
Author:
R. David Gustafson, Jeff Hughes
Publisher:
Cengage Learning

College Algebra
Algebra
ISBN:
9781305115545
Author:
James Stewart, Lothar Redlin, Saleem Watson
Publisher:
Cengage Learning

Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:
9781305071742
Author:
James Stewart, Lothar Redlin, Saleem Watson
Publisher:
Cengage Learning