A large class of 400 students has just taken an exam. The exam consisted of 40 true-false questions each of which was worth one point. TA wants to calculate the conditional probability of the number of correct answers (Y) being equal to 30 given the number of incorrect answers (X) being equal to 10. Which one of the followings will be the correct conditional probability, i.e., P(Y=30|X=10)? 1 P(Y=30|X=10) = 1.0 2 P(Y=30|X=10) = 0.0 3 P(Y=30|X=10) = 0.5 4 P(Y=30|X=10) = 0.9 5 Not enough information
A large class of 400 students has just taken an exam. The exam consisted of 40 true-false questions each of which was worth one point. TA wants to calculate the conditional
|
1
|
P(Y=30|X=10) = 1.0 |
|
2
|
P(Y=30|X=10) = 0.0 |
|
3
|
P(Y=30|X=10) = 0.5 |
|
4
|
P(Y=30|X=10) = 0.9 |
|
5
|
Not enough information |
Random Variable: In probability theory, a random variable is a variable whose values depend on outcomes of a random experiment. It is identified as a measurable function defined on a probability space that maps from a sample space to the real numbers.
Conditional Probability: Let A and B be two events with P(A) > 0. Then the conditional probability of B given A, denoted by P(B | A), is defined as the probability of occurrent of the event B when it is assumed that the event A has already been occurred. It is given by the formula,
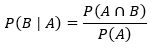
Step by step
Solved in 2 steps with 2 images









