a E R; when a = too, we leave the proof to the reader. Let Sn suplan, an+1,...}; so Sna. By the definition of the limit superior, for each k ≥ 1 there is an mk with a ≤ Smk a, then there are infinitely many values of n such that an> a. = (b) If a € R such that lim sup an a. Thus there is an N such that ank > a for all nk ≥ N. ank (b) If lim sup an
a E R; when a = too, we leave the proof to the reader. Let Sn suplan, an+1,...}; so Sna. By the definition of the limit superior, for each k ≥ 1 there is an mk with a ≤ Smk a, then there are infinitely many values of n such that an> a. = (b) If a € R such that lim sup an a. Thus there is an N such that ank > a for all nk ≥ N. ank (b) If lim sup an
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
Need help with number 4, I have no idea how to do this problem. This is real analysis by the way.

Transcribed Image Text:The text appears to be from a mathematics textbook, focusing on sequences and limits. Below is a transcription tailored for an educational website:
---
**1.3.19 Corollary**: Let \(\{a_n\}\) be a sequence in \(\mathbb{R}\).
(a) If \(a \in \mathbb{R}\) such that \(\limsup a_n > a\), then there are infinitely many values of \(n\) such that \(a_n > a\).
(b) If \(a \in \mathbb{R}\) such that \(\limsup a_n < a\), then there is an integer \(N\) such that \(a_n < a\) for all \(n \geq N\).
**Proof**:
(a) By the preceding proposition there is a subsequence \(\{a_{n_k}\}\) such that \(a_{n_k} \to \limsup a_n > a\). Thus there is an \(N\) such that \(a_{n_k} > a\) for all \(n_k \geq N\).
(b) If \(\limsup a_n < a\), then the definition of the lim sup implies there is an \(N\) with \(\sup\{a_n, a_{n+1}, \dots\} < a\). Hence part (b).
---
**Exercises**:
1. Prove Proposition 1.3.3(b).
2. For each of the following sequences \(\{a_n\}\) find the value of the limit and for each stipulated value of \(\varepsilon\), find a value of \(N\) such that \(|a_n - a| < \varepsilon\) when \(n \geq N\).
(a) \(a_n = n^{-1}\), \(\varepsilon = .0001\), \(a_n = 2^{-n}\), \(\varepsilon = .0001\). (Are the values for \(N\) you found the smallest possible? This has no bearing on the convergence, but it's a bit more challenging to find the smallest possible \(N\).)
3. If \(a_n \to a\) and \(\{a_{n_k}\}\) is a renumbering of the original sequence, does \(a_{n_k}\) converge to \(a
Expert Solution
Step 1: Definition of convergence of sequence
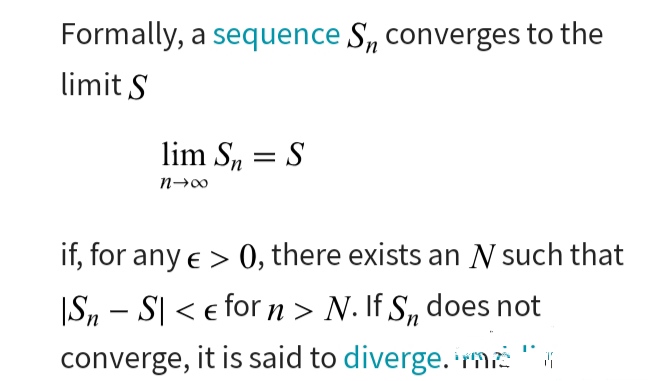
Trending now
This is a popular solution!
Step by step
Solved in 3 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

