A doctor tested two different types (A and B) of stitches. She made nine test stitches (five A 's and 4 B's) and measured the strength of each. From the following strength data (in coded units) she wants to decide whether there is any real difference between the two types. Type A 67 80 106 83 89 Type B 45 71 87 53
A doctor tested two different types (A and B) of stitches. She made nine test stitches (five A 's and 4 B's) and measured the strength of each. From the following strength data (in coded units) she wants to decide whether there is any real difference between the two types.
|
Type A |
67 |
80 |
106 |
83 |
89 |
|
Type B |
45 |
71 |
87 |
53 |
- Use Wilcoxon-Mann-Whitney test to answer this question.
- Use unpaired t-test, assuming equal variances between groups, to answer this question.
- Use unpaired t-test, assuming unequal variances between two groups, to answer this question.
(a). Use Wilcoxon-Mann-Whitney test to test the real difference between the two types:
Given data represents the strengths of Type-A stitches and Type-B stitches.
The investigator is interested to test whether there is no difference in the strengths of Type-A stitches and Type-B stitches.
The null and alternate hypotheses are stated below:
Null hypothesis H0:
H0: There is no significant difference in the strengths of Type-A stitches and Type-B stitches.
Alternative hypothesis H1:
H1: There is a significant difference in the strengths of Type-A stitches and Type-B stitches. (Two tailed test)
Since, the level of significance is not specified, the prior level of significance α = 0.05 can be used.
The required calculations to compute the test statistic are given below:
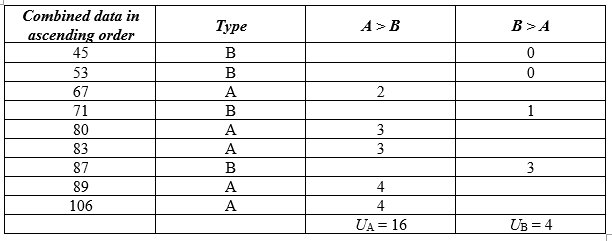
The test statistic is U = minimum (UA, UB) = minimum (16, 4) = 4.
Hence, U = 4.
Critical value:
Here, the sample sizes are n1 = 5 and n2 = 4 and the level of significance is α = 0.05.
From the table values, the critical value is 1.
Decision rule based on critical value approach:
If U ≤ critical value, then reject the null hypothesis H0.
If U > critical value, then fail to reject the null hypothesis H0.
Conclusion based on critical-value approach:
The test statistic U is 4 and critical value is 1.
Here, test statistic value is greater than the critical value.
That is, 4 (= U) > 1 (= critical value).
By the rejection rule, fail to reject the null hypothesis.
Hence, there is no significant difference in the strengths of Type-A stitches and Type-B stitches.
Trending now
This is a popular solution!
Step by step
Solved in 3 steps with 3 images









