A critical point xo, Yo of a function f is obtained when O Vf(x0, Yo) = 0 or Vf(x0, Yo) does not exist O Vf(x0, y0) does not exist O f(r, y) = 0 x O f(ro, Yo) > 0 O Vf(xo, yo) = 0
A critical point xo, Yo of a function f is obtained when O Vf(x0, Yo) = 0 or Vf(x0, Yo) does not exist O Vf(x0, y0) does not exist O f(r, y) = 0 x O f(ro, Yo) > 0 O Vf(xo, yo) = 0
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question

Transcribed Image Text:A critical point \( x_0, y_0 \) of a function \( f \) is obtained when:
- \( \nabla f(x_0, y_0) = 0 \) or \( \nabla f(x_0, y_0) \) does not exist
- \( \nabla f(x_0, y_0) \) does not exist
- \( f(x, y) = 0 \)
- Incorrect: \( f(x_0, y_0) \geq 0 \)
- \( \nabla f(x_0, y_0) = 0 \)
In the list, the fourth option is marked as incorrect.
Expert Solution
Step 1
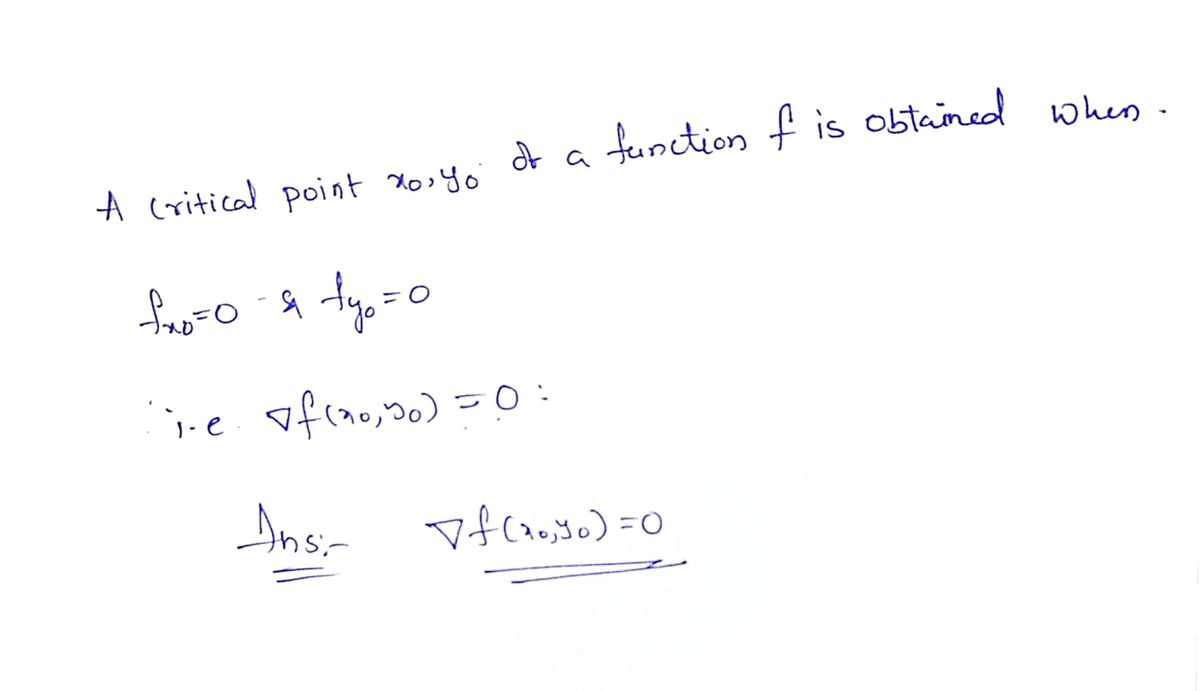
Step by step
Solved in 2 steps with 1 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Similar questions
Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

